Training Optimization for Gate-Model Quantum Neural Networks

Abstract

Gate-based quantum computations represent an essential to realize near-term quantum computer architectures. A gate-model quantum neural network (QNN) is a QNN implemented on a gate-model quantum computer, realized via a set of unitaries with associated gate parameters. Here, we define a training optimization procedure for gate-model QNNs. By deriving the environmental attributes of the gate-model quantum network, we prove the constraint-based learning models. We show that the optimal learning procedures are different if side information is available in different directions, and if side information is accessible about the previous running sequences of the gate-model QNN. The results are particularly convenient for gate-model quantum computer implementations.

Introduction

Gate-based quantum computers represent an implementable way to realize experimental quantum computations on near-term quantum computer architectures^{1,2,3,4,5,6,7,8,9,10,11,12,13}. In a gate-model quantum computer, the transformations are realized by quantum gates, such that each quantum gate is represented by a unitary operation^{14,15,16,17,18,19,20,21,22,23,24,25,26}. An input quantum state is evolved through a sequence of unitary gates and the output state is then assessed by a measurement operator^14,15,16,17. Focusing on gate-model quantum computer architectures is motivated by the successful demonstration of the practical implementations of gate-model quantum computers^7,8,9,10,11, and several important developments for near-term gate-model quantum computations are currently in progress. Another important aspect is the application of gate-model quantum computations in the near-term quantum devices of the quantum Internet^{27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43}.

A quantum neural network (QNN) is formulated by a set of quantum operations and connections between the operations with a particular weight parameter^{14,25,26,44,45,46,47}. Gate-model QNNs refer to QNNs implemented on gate-model quantum computers¹⁴. As a corollary, gate-model QNNs have a crucial experimental importance since these network structures are realizable on near-term quantum computer architectures. The core of a gate-model QNN is a sequence of unitary operations. A gate-model QNN consists of a set of unitary operations and communication links that are used for the propagation of quantum and classical side information in the network for the related calculations of the learning procedure. The unitary transformations represent quantum gates parameterized by a variable referred to as gate parameter (weight). The inputs of the gate-model QNN structure are a computational basis state and an auxiliary quantum system that serves a readout state in the output measurement phase. Each input state is associated with a particular label. In the modeled learning problem, the training of the gate-model QNN aims to learn the values of the gate parameters associated with the unitaries so that the predicted label is close to a true label value of the input (i.e., the difference between the predicted and true values is minimal). This problem, therefore, formulates an objective function that is subject to minimization. In this setting, the training of the gate-model QNN aims to learn the label of a general quantum state.

In artificial intelligence, machine learning^{4,5,6,19,23,45,46,48,49,50,51,52,53} utilizes statistical methods with measured data to achieve a desired value of an objective function associated with a particular problem. A learning machine is an abstract computational model for the learning procedures. A constraint machine is a learning machine that works with constraint, such that the constraints are characterized and defined by the actual environment⁴⁸.

The proposed model of a gate-model quantum neural network assumes that quantum information can only be propagated forward direction from the input to the output, and classical side information is available via classical links. The classical side information is processed further via a post-processing unit after the measurement of the output. In the general gate-model QNN scenario, it is assumed that classical side information can be propagated arbitrarily in the network structure, and there is no available side information about the previous running sequences of the gate-model QNN structure. The situation changes, if side information propagates only backward direction and side information about the previous running sequences of the network is also available. The resulting network model is called gate-model recurrent quantum neural network (RQNN).

Here, we define a constraint-based training optimization method for gate-model QNNs and RQNNs, and propose the computational models from the attributes of the gate-model quantum network environment. We show that these structural distinctions lead to significantly different computational models and learning optimization. By using the constraint-based computational models of the QNNs, we prove the optimal learning methods for each network—nonrecurrent and recurrent gate-model QNNs—vary. Finally, we characterize optimal learning procedures for each variant of gate-model QNNs.

The novel contributions of our manuscript are as follows.

• We study the computational models of nonrecurrent and recurrent gate-model QNNs realized via an arbitrary number of unitaries.

• We define learning methods for nonrecurrent and recurrent gate-model QNNs.

• We prove the optimal learning for nonrecurrent and recurrent gate-model QNNs.

This paper is organized as follows. In Section 2, the related works are summarized. Section 3 defines the system model and the parameterization of the learning optimization problem. Section 4 proves the computational models of gate-model QNNs. Section 5 provides learning optimization results. Finally, Section 6 concludes the paper. Supplemental information is included in the Appendix.

Related Works

Gate-model quantum computers

A theoretical background on the realizations of quantum computations in a gate-model quantum computer environment can be found in¹⁵ and¹⁶. For a summary on the related references^{1,2,3,13,15,16,17,54,55}, we suggest⁵⁶.

Quantum neural networks

In¹⁴, the formalism of a gate-model quantum neural network is defined. The gate-model quantum neural network is a quantum neural network implemented on gate-model quantum computer. A particular problem analyzed by the authors is the classification of classical data sets which consist of bitstrings with binary labels.

In⁴⁴, the authors studied the subject of quantum deep learning. As the authors found, the application of quantum computing can reduce the time required to train a deep restricted Boltzmann machine. The work also concluded that quantum computing provides a strong framework for deep learning, and the application of quantum computing can lead to significant performance improvements in comparison to classical computing.

In⁴⁵, the authors defined a quantum generalization of feedforward neural networks. In the proposed system model, the classical neurons are generalized to being quantum reversible. As the authors showed, the defined quantum network can be trained efficiently using gradient descent to perform quantum generalizations of classical tasks.

In⁴⁶, the authors defined a model of a quantum neuron to perform machine learning tasks on quantum computers. The authors proposed a small quantum circuit to simulate neurons with threshold activation. As the authors found, the proposed quantum circuit realizes a “œquantum neuron”. The authors showed an application of the defined quantum neuron model in feedforward networks. The work concluded that the quantum neuron model can learn a function if trained with superposition of inputs and the corresponding output. The proposed training method also suffices to learn the function on all individual inputs separately.

In²⁵, the authors studied the structure of artificial quantum neural network. The work focused on the model of quantum neurons and studied the logical elements and tests of convolutional networks. The authors defined a model of an artificial neural network that uses quantum-mechanical particles as a neuron, and set a Monte-Carlo integration method to simulate the proposed quantum-mechanical system. The work also studied the implementation of logical elements based on introduced quantum particles, and the implementation of a simple convolutional network.

In²⁶, the authors defined the model of a universal quantum perceptron as efficient unitary approximators. The authors studied the implementation of a quantum perceptron with a sigmoid activation function as a reversible many-body unitary operation. In the proposed system model, the response of the quantum perceptron is parameterized by the potential exerted by other neurons. The authors showed that the proposed quantum neural network model is a universal approximator of continuous functions, with at least the same power as classical neural networks.

Quantum machine learning

In⁵⁷, the authors analyzed a Markov process connected to a classical probabilistic algorithm⁵⁸. A performance evaluation also has been included in the work to compare the performance of the quantum and classical algorithm.

In¹⁹, the authors studied quantum algorithms for supervised and unsupervised machine learning. This particular work focuses on the problem of cluster assignment and cluster finding via quantum algorithms. As a main conclusion of the work, via the utilization of quantum computers and quantum machine learning, an exponential speed-up can be reached over classical algorithms.

In²⁰, the authors defined a method for the analysis of an unknown quantum state. The authors showed that it is possible to perform “œquantum principal component analysis” by creating quantum coherence among different copies, and the relevant attributes can be revealed exponentially faster than it is possible by any existing algorithm.

In²¹, the authors studied the application of a quantum support vector machine in Big Data classification. The authors showed that a quantum version of the support vector machine (optimized binary classifier) can be implemented on a quantum computer. As the work concluded, the complexity of the quantum algorithm is only logarithmic in the size of the vectors and the number of training examples that provides a significant advantage over classical support machines.

In²², the problem of quantum-based analysis of big data sets is studied by the authors. As the authors concluded, the proposed quantum algorithms provide an exponential speedup over classical algorithms for topological data analysis.

The problem of quantum generative adversarial learning is studied in⁵¹. In generative adversarial networks a generator entity creates statistics for data that mimics those of a valid data set, and a discriminator unit distinguishes between the valid and non-valid data. As a main conclusion of the work, a quantum computer allows us to realize quantum adversarial networks with an exponential advantage over classical adversarial networks.

In⁵⁴, super-polynomial and exponential improvements for quantum-enhanced reinforcement learning are studied.

In⁵⁵, the authors proposed strategies for quantum computing molecular energies using the unitary coupled cluster ansatz.

The authors of⁵⁶ provided demonstrations of quantum advantage in machine learning problems.

In⁵⁷, the authors study the subject of quantum speedup in machine learning. As a particular problem, the work focuses on finding Boolean functions for classification tasks.

System Model

Gate-model quantum neural network

Definition 1 A QNN_QG is a quantum neural network (QNN) implemented on a gate-model quantum computer with a quantum gate structure QG. It contains quantum links between the unitaries and classical links for the propagation of classical side information. In a QNN_QG, all quantum information propagates forward from the input to the output, while classical side information can propagate arbitrarily (forward and backward) in the network. In a QNN_QG, there is no available side information about the previous running sequences of the structure.

Using the framework of¹⁴, a QNN_QG is formulated by a collection of L unitary gates, such that an i-th, i = 1, …, L unitary gate U_i(θ_i) is

$${U}_{i}({\theta }_{i})=\exp (-i{\theta }_{i}P),$$

(1)

where P is a generalized Pauli operator formulated by a tensor product of Pauli operators {X, Y, Z}, while θ_i is referred to as the gate parameter associated with U_i(θ_i).

In QNN_QG, a given unitary gate U_i(θ_i) sequentially acts on the output of the previous unitary gate U_i−1(θ_i−1), without any nonlinearities¹⁴. The classical side information of QNN_QG is used in calculations related to error derivation and gradient computations, such that side information can propagate arbitrarily in the network structure.

The sequential application of the L unitaries formulates a unitary operator $U(\overrightarrow{\theta })$ as

$$U(\overrightarrow{\theta })={U}_{L}({\theta }_{L}){U}_{L-1}({\theta }_{L-1})\ldots {U}_{1}({\theta }_{1}),$$

(2)

where U_i(θ_i) identifies an i-th unitary gate, and $\overrightarrow{\theta }$ is the gate parameter vector

$$\overrightarrow{\theta }={({\theta }_{1},\ldots ,{\theta }_{L-1},{\theta }_{L})}^{T}.$$

(3)

At (2), the evolution of the system of QNN_QG for a particular input system $|\psi ,\varphi \rangle$ is

$$|Y\rangle =U(\overrightarrow{\theta })|\psi \rangle |\varphi \rangle =U(\overrightarrow{\theta })|z\rangle |1\rangle =U(\overrightarrow{\theta })|z\mathrm{,}\,1\rangle ,$$

(4)

where $|Y\rangle$ is the (n + 1)-length output quantum system, and $|\psi \rangle =|z\rangle$ is a computational basis state, where z is an n-length string

$$z={z}_{1}{z}_{2}\ldots {z}_{n},$$

(5)

where each z_i represents a classical bit with values

$${z}_{i}\in \{\,-\,\mathrm{1,}\,1\},$$

(6)

while the (n + 1)-th quantum state is initialized as

$$|\varphi \rangle =|1\rangle ,$$

(7)

and is referred to as the readout quantum state.

Objective function

The $f(\overrightarrow{\theta })$ objective function subject to minimization is defined for a QNN_QG as

$$f(\overrightarrow{\theta })=\langle \overrightarrow{\theta }| {\mathcal L} ({x}_{0},\tilde{l}(z))|\overrightarrow{\theta }\rangle ,$$

(8)

where ${\mathcal L} ({x}_{0},\tilde{l}(z))$ is the loss function¹⁴, defined as

$$ {\mathcal L} ({x}_{0},\tilde{l}(z))=1-l(z)\tilde{l}(z),$$

(9)

where $\tilde{l}(z)$ is the predicted value of the binary label

$$l(z)\in \{-\mathrm{1,}\,1\}$$

(10)

of the string z, defined as¹⁴

$$\tilde{l}(z)=\langle z\mathrm{,1|(}U(\overrightarrow{\theta }{))}^{\dagger }{Y}_{n+1}U(\overrightarrow{\theta })|z\mathrm{,}\,1\rangle ,$$

(11)

where Y_n+1 ∈ {−1, 1} is a measured Pauli operator on the readout quantum state (7), while x₀ is as

$${x}_{0}=|z,1\rangle .$$

(12)

The $\tilde{l}$ predicted value in (11) is a real number between −1 and 1, while the label l(z) and Y_n+1 are real numbers −1 or 1. Precisely, the $\tilde{l}$ predicted value as given in (11) represents an average of several measurement outcomes if Y_n+1 is measured via R output system instances |Y〉^(r)-s, r = 1, …, R¹⁴.

The learning problem for a QNN_QG is, therefore, as follows. At an ${{\mathscr{S}}}_{T}$ training set formulated via R input strings and labels

$${{\mathscr{S}}}_{T}=\{{z}^{(r)},l({z}^{(r)}),r=1,\ldots ,R\},$$

(13)

where r refers to the r-th measurement round and R is the total number of measurement rounds, the goal is therefore to find the gate parameters (3) of the L unitaries of QNN_QG, such that $f(\overrightarrow{\theta })$ in (8) is minimal.

Recurrent Gate-model quantum neural network

Definition 2 An RQNN_QG is a QNN implemented on a gate-model quantum computer with a quantum gate structure QG, such that the connections of RQNN_QG form a directed graph along a sequence. It contains quantum links between the unitaries and classical links for the propagation of classical side information. In an RQNN_QG, all quantum information propagates forward, while classical side information can propagate only backward direction. In an RQNN_QG, side information is available about the previous running sequences of the structure.

The classical side information of RQNN_QG is used in error derivation and gradient computations, such that side information can propagate only in backward directions. Similar to the QNN_QG case, in an RQNN_QG, a given i-th unitary U_i(θ_i) acts on the output of the previous unitary U_i−1(θ_i−1). Thus, the quantum evolution of the RQNN_QG contains no nonlinearities¹⁴. As follows, for an RQNN_QG network, the objective function can be similarly defined as given in (8). On the other hand, the structural differences between QNN_QG and RQNN_QG allows the characterization of different computational models for the description of the learning problem. The structural differences also lead to various optimal learning methods for the QNN_QG and RQNN_QG structures as it will be revealed in Section 4 and Section 5.

Comparative representation

For a simple graphical representation, the schematic models of a QNN_QG and RQNN_QG for an (r − 1)-th and r-th measurement rounds are compared in Fig. 1. The (n + 1)-length input systems are depicted by $|{\psi }_{r-1}\rangle |1\rangle$ and $|{\psi }_{r}\rangle |1\rangle$, while the output systems are denoted by $|{Y}_{r-1}\rangle$ and $|{Y}_{r}\rangle$. The result of the M measurement operator in the (r − 1)-th and r-th measurement rounds are denoted by ${Y}_{n+1}^{(r-1)}$ and ${Y}_{n+1}^{(r)}$. In Fig. 1(a), structure of a QNN_QG is depicted for an (r − 1)-th and r-th measurement round. In Fig. 1(b), the structure of a RQNN_QG is illustrated. In a QNN_QG, side information is not available about the previous, (r − 1)-th measurement round in a particular r-th measurement round. For an RQNN_QG, side information is available about the (r − 1)-th measurement round (depicted by the dashed gray arrows) in a particular r-th measurement round. The side information in the RQNN_QG setting refer to information about the gate-parameters and the measurement results of the (r − 1)-th measurement round.

Figure 1

Schematic representation of a QNN_QG and RQNN_QG in an (n − 1)-th and r-th measurement rounds. The (n + 1)-length input systems of the (r − 1) and r-th measurement rounds are depicted by $|{\psi }_{r-1}\rangle |1\rangle$ and $|{\psi }_{r}\rangle |1\rangle$, the output systems are $|{Y}_{r-1}\rangle$ and $|{Y}_{r}\rangle$. The result of the M measurement operator in the (n − 1)-th and r-th measurement rounds are denoted by ${Y}_{n+1}^{(r-1)}$ and ${Y}_{n+1}^{(r)}$. (a) In a QNN_QG, for an r-th measurement round, side information is not available about the previous (n − 1)-th measurement round. (b) In a RQNN_QG, side information is available about the previous (n − 1)-th measurement round in an r-th round.

Parameterization

Constraint machines

The tasks of machine learning can be modeled via its mathematical framework and the constraints of the environment^4,5,6. A ${\mathscr{C}}$ constraint machine is a learning machine working with constraints⁴⁸. A constraint machine can be formulated by a particular function f or via some elements of a functional space ${\mathcal F}$. The constraints model the attributes of the environment of ${\mathscr{C}}$.

The learning problem of a ${\mathscr{C}}$ constraint machine can be represented via a ${\mathscr{G}}=(V,S)$ environmental graph^{48,59,60,61,62}. The ${\mathscr{G}}$ environmental graph is a directed acyclic graph (DAG), with a set V of vertexes and a set S of arcs. The vertexes of ${\mathscr{G}}$ model associated features, while the arcs between the vertexes describe the relations of the vertexes.

The ${\mathscr{G}}$ environmental graph formalizes factual knowledge via modeling the relations among the elements of the environment⁴⁸. In the environmental graph representation, the ${\mathscr{C}}$ constraint machine has to decide based on the information associated with the vertexes of the graph.

For any vertex v of V, a perceptual space element x, and its identifier 〈x〉 that addresses x in the computational model can be defined as a pair

$$(\langle x\rangle ,x),$$

(14)

where $x\in {\mathscr{X}}$ is an element (vector) of the perceptual space ${\mathscr{X}}\subset {{\mathbb{C}}}^{d}$. Assuming that features are missing, the ◊ symbol can be used. Therefore, ${\mathscr{X}}$ is initialized as ${{\mathscr{X}}}_{0}$,

$${{\mathscr{X}}}_{0}={\mathscr{X}}\cup \{\diamond \}.$$

(15)

The environment is populated by individuals, and the ${\mathcal I}$ individual space is defined via V and ${{\mathscr{X}}}_{0}$ as

$$ {\mathcal I} =V\times {{\mathscr{X}}}_{0},$$

(16)

such that the existing features are associated with a subset $\tilde{V}$ of V.

The features can be associated with the 〈x〉 identifier via a ${f}_{{\mathscr{P}}}$ perceptual map as

$${f}_{{\mathscr{P}}}:\tilde{V}\to {\mathscr{X}}\,:\,:x={f}_{{\mathscr{P}}}(v).$$

(17)

If the condition

$$\forall v\in (V\backslash \tilde{V}):x={f}_{{\mathscr{P}}}(v)=\diamond $$

(18)

holds, then ${f}_{{\mathscr{P}}}$ is yielded as

$${f}_{{\mathscr{P}}}:V\to {\mathscr{X}}\,:\,:x={f}_{{\mathscr{P}}}(v).$$

(19)

A given individual $\iota \in {\mathcal I}$ is defined as a feature vector $x\in {\mathscr{X}}$. An $\iota \in {\mathcal I}$ individual of the individual space ${\mathcal I}$ is defined as

$$\iota =\Upsilon x+\neg \Upsilon v,$$

(20)

where + is the sum operator in ${{\mathbb{C}}}^{d}$, ¬ is the negation operator, while Υ is a constraint as

$$\Upsilon :(v\in \tilde{V})\vee (x\in {\mathscr{X}}\,\backslash {\tilde{{\mathscr{X}}}}_{0}).$$

(21)

where ${{\mathscr{X}}}_{0}$ is given in (15). Thus, from (20), an individual ι is a feature vector x of ${\mathscr{X}}$ or a vertex v of ${\mathscr{G}}$.

Let ${\iota }^{\ast }\in {\mathcal I}$ be a specific individual, and let f be an agent represented by the function $f: {\mathcal I} \to {{\mathbb{C}}}^{n}$. Then, at a given environmental graph ${\mathscr{G}}$, the ${\mathscr{C}}$ constraint machine is defined via function f as a machine in which the learning and inference are represented via enforcing procedures on constraints ${C}_{{\iota }^{\ast }}$ and C_ι, such that for a ${\mathscr{C}}$ constraint machine the learning procedure requires the satisfaction of the constraints over all ${ {\mathcal I} }^{\ast }$, while in the inference the satisfaction of the constraint is enforced over the given ${\iota }^{\ast }\in {\mathcal I}$⁴⁸, by theory. Thus, ${\mathscr{C}}$ is defined in a formalized manner, as

$${\mathscr{C}}\equiv \{\begin{array}{l}{C}_{\iota }\,:\forall \iota \in \tilde{ {\mathcal I} }\,:\chi (v,f(\iota ))=\mathrm{0,}\\ {C}_{\iota \ast }\,:{\iota }^{\ast }\in {\mathcal I} \,\backslash \tilde{ {\mathcal I} }\,:\chi ({v}^{\ast },{f}^{\ast }({\iota }^{\ast }))=\mathrm{0,}\end{array}$$

(22)

where $\tilde{ {\mathcal I} }$ is a subset of ${\mathcal I}$, ι^* refers to a specific individual, vertex or function, χ(⋅) is a compact constraint function, while v^* and f^*(ι^*) refer to the vertex and function at ι^*, respectively.

Calculus of variations

Some elements from the calculus of variations^63,64 are utilized in the learning optimization procedure.

Euler-Lagrange Equations: The Euler-Lagrange equations are second-order partial differential equations with solution functions. These equations are useful in optimization problems since they have a differentiable functional that is stationary at the local maxima and minima⁶³. As a corollary, they can be also used in the problems of machine learning.

Hessian Matrix: A Hessian matrix H is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field⁶³. In theory, it describes the local curvature of a function of many variables. In a machine-learning setting, it is a useful tool to derive some attributes and critical points of loss functions.

Constraint-based Computational Model

In this section, we derive the computational models of the QNN_QG and RQNN_QG structures.

Environmental graph of a gate-model quantum neural network

Proposition 1 The ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}=(V,S)$ environmental graph of a QNN_QG is a DAG, where V is a set of vertexes, in our setting defined as

$$V={{\mathscr{S}}}_{in}\cup {\mathscr{U}}\cup {\mathscr{Y}},$$

(23)

where ${{\mathscr{S}}}_{in}$ is the input space, ${\mathscr{U}}$ is the space of unitaries, ${\mathscr{Y}}$ is the output space, and S is a set of arcs.

Let ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$ be an environmental graph of QNN_QG, and let ${v}_{{U}_{i}}$ be a vertex, such that ${v}_{{U}_{i}}\in V$ is related to the unitary U_i(θ_i), where index i = 0 is associated with the $|z\mathrm{,\; 1}\rangle$ input system with vertex v₀. Then, let ${v}_{{U}_{i}}$ and ${v}_{{U}_{j}}$ be connected vertices via directed arc s_ij, s_ij ∈ S, such that a particular θ_ij gate parameter is associated with the forward directed arc (Note: the notation U_j(θ_ij) refers to the selection of θ_j for the unitary U_j to realize the operation U_i(θ_i)U_j(θ_j), i.e., the application of U_j(θ_j) on the output of U_i(θ_i) at a particular gate parameter θ_j), as

$${\theta }_{ij}={\theta }_{j},$$

(24)

such that arc s_0j is associated with θ_0j = θ_j.

Then a given state ${x}_{{U}_{i}({\theta }_{i})}$ of ${\mathscr{X}}$ associated with U_i(θ_i) is defined as

$${x}_{{U}_{i}({\theta }_{i})}={v}_{{U}_{i}}+{a}_{{U}_{i}({\theta }_{i})},$$

(25)

where ${v}_{{U}_{i}}$ is a label for unitary U_i in the environmental graph ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$ (serves as an identifier in the computational structure of (25)), while parameter ${a}_{{U}_{i}({\theta }_{i})}$ is defined for a U_i(θ_i) as

$${a}_{{U}_{i}({\theta }_{i})}=\sum _{h\in {\rm{\Xi }}(i)}{U}_{i}({\theta }_{hi}){x}_{{U}_{h}({\theta }_{h})}+{b}_{{U}_{i}({\theta }_{i})},$$

(26)

where Ξ(i) refers to the parent set of ${v}_{{U}_{i}}$, U_i(θ_hi) refers to the selection of θ_i for unitary U_i for a particular input from U_h(θ_h), while ${b}_{{U}_{i}({\theta }_{i})}$ is the bias relative to ${v}_{{U}_{i}}$.

Applying a f_∠ topological ordering function on ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$ yields an ordered graph structure ${f}_{\angle }({{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}})$ of the L unitaries. Thus, a given output $|Y\rangle$ of QNN_QG can be rewritten in a compact form as

$$|Y\rangle =U(\overrightarrow{\theta }){x}_{0}=({U}_{L}({\theta }_{L}){U}_{L-1}({\theta }_{L-1})\ldots {U}_{1}({\theta }_{1}){x}_{0}),$$

(27)

where the term ${x}_{0}\in {{\mathscr{S}}}_{in}$ is associated with the input system as defined in (12).

A particular state ${x}_{{U}_{l}({\theta }_{l})}$, l = 1, …, L is evaluated in function of ${x}_{{U}_{l-1}({\theta }_{l-1})}$ as

$${x}_{{U}_{l}({\theta }_{l})}={U}_{l}({\theta }_{l}){x}_{{U}_{l-1}({\theta }_{l-1})}.$$

(28)

The environmental and ordered graphs of a gate-model quantum neural network are illustrated in Fig. 2. In Fig. 2(a) the ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$ environmental graph of a QNN_QG is depicted, and the ordered graph ${f}_{\angle }({{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}})$ is shown in Fig. 2(b).

Figure 2

(a) The ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ environmental graph of a QNN_QG, with L unitaries. The input state of the QNN_QG is $|\psi \mathrm{,1}\rangle$. A unitary U_i(θ_i) is represented by a vertex ${v}_{{U}_{i}}$ in ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$. The vertices ${v}_{{U}_{i}}$ and ${v}_{{U}_{j}}$ of unitaries U_i(θ_i) and U_j(θ_j) are connected by directed arcs s_ij. The gate parameters θ_ij = θ_j are associated with s_ij, while ${{\mathscr{S}}}_{in}$ is the input space, ${\mathscr{U}}$ is the space of L unitaries, and ${\mathscr{Y}}$ is the output space. Operator M is a measurement on the (n + 1)-th state (readout quantum state), and Y_n+1 is a Pauli operator measured on the readout state (classical links are not depicted) (b) The compacted ordered graph ${f}_{\angle }({{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}})$ of QNN_QG. The output is $|Y\rangle =U(\overrightarrow{\theta }){x}_{0}$, where ${x}_{0}=|z\mathrm{,1}\rangle$ and $U(\overrightarrow{\theta })={\prod }_{l=1}^{L}{U}_{l}({\theta }_{l})$ (classical links are not depicted).

Computational model of gate-model quantum neural networks

Theorem 1

The computational model of a QNN_QG is a ${\mathscr{C}}({\rm{Q}}N{N}_{QG})$ constraint machine with linear transition functions f_T(QNN_QG).

Proof. Let ${\mathscr{G}}({\rm{Q}}N{N}_{QG})=(V,S)$ be the environmental graph of a QNN_QG, and assume that the number of types of the vertexes is p. Then, the vertex set V can be expressed as a collection

$$V=\underset{i=1}{\overset{p}{\cup }}{V}_{i},$$

(29)

where V_i identifies a set of vertexes, p is the total number of the V_i sets, such that ${V}_{i}\cap {V}_{j}=\varnothing ,$ if only i ≠ j⁴⁸. For a v ∈ V_i vertex from set V_i, an ${f}_{T}:{{\mathbb{C}}}^{{{\rm{\dim }}}_{in}}\to {{\mathbb{C}}}^{{{\rm{\dim }}}_{out}}$ transition function⁴⁸ can be defined as

$${f}_{T}:{{\mathscr{Z}}}_{{V}_{i}}^{|{\rm{\Gamma }}(v)|}\times {{\mathscr{X}}}_{{V}_{i}}\to {{\mathscr{Z}}}_{{V}_{i}}:({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v})\to {f}_{T}({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v}),$$

(30)

where ${{\mathscr{X}}}_{{V}_{i}}$ is the perceptual space ${\mathscr{X}}$ of V_i, ${{\mathscr{Z}}}_{{V}_{i}}\subset {{\mathbb{C}}}^{{\rm{\dim }}({{\mathscr{Z}}}_{{V}_{i}})}$; ${\rm{\dim }}({{\mathscr{Z}}}_{{V}_{i}})$ is the dimension of the space ${{\mathscr{Z}}}_{{V}_{i}}$; x_v is an element of ${{\mathscr{X}}}_{{V}_{i}}$; ${x}_{v}\in {{\mathscr{X}}}_{{V}_{i}}$ associated with a unitary U_v(θ_v); ${\mathscr{Z}}$ is the state space, ${{\mathscr{Z}}}_{{V}_{i}}$ is the state space of V_i, ${{\mathscr{Z}}}_{{V}_{i}}\subset {{\mathbb{C}}}^{{\rm{d}}{\rm{i}}{\rm{m}}({{\mathscr{Z}}}_{{V}_{i}})}$, ${\rm{d}}{\rm{i}}{\rm{m}}({{\mathscr{Z}}}_{{V}_{i}})$ is the dimension of the space ${{\mathscr{Z}}}_{{V}_{i}}$; Γ(v) refers to the children set of v; |Γ(v)| is the cardinality of set Γ(v); $\gamma \in {\mathscr{Z}}$ is a state variable in the state space ${\mathscr{Z}}$ that serves as side information to process the v vertices of V in ${\mathscr{G}}({{\rm{QNN}}}_{QG})$, while ${\gamma }_{{\rm{\Gamma }}(v)}\in {{\mathscr{Z}}}_{{V}_{i}}^{|{\rm{\Gamma }}(v)|}\subset {{\mathbb{C}}}^{|{\rm{\Gamma }}(v)|}$ and ${\gamma }_{{\rm{\Gamma }}(v)}=({\gamma }_{{\rm{\Gamma }}(v\mathrm{),1}},\cdots ,{\gamma }_{{\rm{\Gamma }}(v),|{\rm{\Gamma }}(v)|})$, by theory^48,62. Thus, the f_T transition function in (30) is a complex-valued function that maps an input pair (γ, x) from the space of ${\mathscr{X}}\times {\mathscr{Z}}$ to the state space ${\mathscr{Z}}$.

Similarly, for any V_i, an ${f}_{O}:{{\mathbb{C}}}^{{{\rm{\dim }}}_{in}}\to {{\mathbb{C}}}^{{{\rm{\dim }}}_{out}}$ output function⁴⁸ can be defined as

$${F}_{O}:{{\mathscr{Z}}}_{{V}_{i}}\times {{\mathscr{X}}}_{{V}_{i}}\to {{\mathscr{Y}}}_{{V}_{i}}:({\gamma }_{v},{x}_{v})\to {F}_{O}({\gamma }_{v},{x}_{v}),$$

(31)

where ${{\mathscr{Y}}}_{{V}_{i}}$ is the output space ${\mathscr{Y}}$, and γ_v is a state variable associated with v, ${\gamma }_{v}\in {{\mathscr{Z}}}_{{V}_{i}}$, such that γ_v = γ₀ if ${\rm{\Gamma }}(v)=\varnothing$. The f_O output function in (31) is therefore a complex-valued function that maps an input pair (γ, x) from the space of ${\mathscr{X}}\times {\mathscr{Z}}$ to the output space ${\mathscr{Y}}$.

From (30) and (31), it follows that for any V_i, there exists the ϕ(V_i) associated function-pair as

$$\varphi ({V}_{i})=({f}_{T},{F}_{O}).$$

(32)

Let us specify the generalized functions of (30) and (31) for a QNN_QG.

Let $U(\overrightarrow{\theta })$ of QNN_QG be defined as given in (2). Since in QNN_QG, a given i-th unitary U_i(θ_i) acts on the output of the previous unitary U_i−1(θ_i−1), the network contains no nonlinearities¹⁴. As a corollary, the state transition function f_T(QNN_QG) in (30) is also linear for a QNN_QG.

Let $|{\gamma }_{v}\rangle$ be the quantum state associated with γ_v state variable of a given v. Then, the constraints on the transition function and output function of a QNN_QG can be evaluated as follows.

Let f_T(QNN_QG) be the transition function of a QNN_QG defined for a given v ∈ V of ${\mathscr{G}}({{\rm{QNN}}}_{QG})$ via (30) as

$${f}_{T}({{\rm{QNN}}}_{QG}):({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v})\to {f}_{T}({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v}).$$

(33)

The F_O(QNN_QG) output function of a QNN_QG for a given v of ${\mathscr{G}}({{\rm{QNN}}}_{QG})$ via (31) is

$${F}_{O}({{\rm{QNN}}}_{QG}):({\gamma }_{v},{x}_{v})\to {F}_{O}({\gamma }_{v},{x}_{v}).$$

(34)

Since f_T(QNN_QG) in (33) and F_O(QNN_QG) in (34) correspond with the data flow computational scheme of a QNN_QG with linear transition functions, (33) and (34) represent an expression of the constraints of QNN_QG. These statements can be formulated in a compact form.

Let ζ_v be a constraint on f_T(QNN_QG) of QNN_QG as

$${\zeta }_{v}:|{\gamma }_{v}\rangle -{f}_{T}({\rm{Q}}N{N}_{QG})=0.$$

(35)

Thus, the f_T(QNN_QG) transition function is constrained as

$${f}_{T}({{\rm{QNN}}}_{QG})=|{\gamma }_{v}\rangle .$$

(36)

With respect to the output function, let φ_v be a constraint on F_O(QNN_QG) of QNN_QG as

$${\phi }_{v}:{\wp }_{v}\circ {F}_{O}({{\rm{QNN}}}_{QG})=0,$$

(37)

where ⚬ is the composition operator, such that $(f\circ g)(x)=f(g(x))$, ${\wp }_{v}$ is therefore another constraint as ${\wp }_{v}({F}_{O}({{\rm{QNN}}}_{QG}))=0$.

Then let π_v be a compact constraint on f_T(QNN_QG) and F_O(QNN_QG) defined via constraints (35) and (37) as

$$\begin{array}{lll}{\pi }_{v}({f}_{T}({{\rm{QNN}}}_{QG}),{F}_{O}({{\rm{QNN}}}_{QG})) & & \\ & = & \sum _{v\in V}({\zeta }_{v}+{\phi }_{v})-2|V|\\ & = & \sum _{v\in V}((|{\gamma }_{v}\rangle -({f}_{T}({{\rm{QNN}}}_{QG}))+{\wp }_{v}({F}_{O}({\rm{Q}}N{N}_{QG})))-2|V|\\ & \ne & 0.\end{array}$$

(38)

Since it can be verified that a learning machine that enforces the constraint in (38), is in fact a constraint machine. As a corollary, the constraints (33) and (34), along with the compact constraint (38), define a ${\mathscr{C}}({{\rm{QNN}}}_{QG})$ constraint machine for a QNN_QG with linear functions f_T(QNN_QG) and F_O(QNN_QG).■

Diffusion machine

Let ${\mathscr{C}}$ be the constraint machine with linear transition function f_T(γ_Γ(v), x_v), and let §_v be a state variable such that $\forall \,v\in V$

$${\S }_{v}-{f}_{T}({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v})=0,$$

(39)

and let F_O(γ_v, x_v) be the output function of ${\mathscr{C}}$, such that ∀v ∈ V

$${c}_{v}\circ {F}_{O}({\gamma }_{v},{x}_{v})=0,$$

(40)

where c_v is a constraint.

Then, the ${\mathscr{C}}$ constraint machine is a ${\mathscr{D}}$ diffusion machine⁴⁸, if only ${\mathscr{C}}$ enforces the constraint ${C}_{{\mathscr{D}}}$, as

$${C}_{{\mathscr{D}}}:\sum _{v\in V}(({\S }_{v}-{f}_{T}({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v})=0)+({c}_{v}\circ {F}_{O}({\gamma }_{v},{x}_{v})=\mathrm{0)})-\,2|V|=0.$$

(41)

Computational model of recurrent gate-model quantum neural networks

Theorem 2

The computational model of an RQNN_QG is a ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$ diffusion machine with linear transition functions f_T(RQNN_QG).

Proof. Let ${\mathscr{C}}({{\rm{RQNN}}}_{QG})$ be the constraint machine of RQNN_QG with linear transition function f_T(RQNN_QG) = f_T(γ_Γ(v), x_v). Using the ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ environmental graph, let Λ_v be a constraint on f_T(RQNN_QG) of RQNN_QG, v ∈ V as

$${{\rm{\Lambda }}}_{v}:|{\gamma }_{v}\rangle -{f}_{T}({{\rm{RQNN}}}_{QG})=0,$$

(42)

where $|{\gamma }_{v}\rangle$ is the quantum state associated with γ_v state variable of a given v of RQNN_QG. With respect to the output function F_O(RQNN_QG) = F_O(γ_v, x_v) of RQNN_QG, let ω_v be a constraint on F_O(RQNN_QG) of RQNN_QG, as

$${\omega }_{v}:{{\rm{\Omega }}}_{v}\circ {F}_{O}({{\rm{RQNN}}}_{QG})=0,$$

(43)

where Ω_v is another constraint as Ω_v(F_O(RQNN_QG)) = 0.

Since RQNN_QG is a recurrent network, for all v ∈ V of ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$, a diffuse constraint λ(Q(x)) can be defined via constraints (42) and (43), as

$$\begin{array}{lll}\lambda (Q(x)) & & \\ & = & \sum _{v\in V}({{\rm{\Lambda }}}_{v}+{\omega }_{v})-2|V|\\ & = & \sum _{v\in V}((|{\gamma }_{v}\rangle -({f}_{T}({{\rm{RQNN}}}_{QG}))+{{\rm{\Omega }}}_{v}({F}_{O}({{\rm{RQNN}}}_{QG})))-2|V|\\ & = & \mathrm{0,}\end{array}$$

(44)

where x = (x₁, …, x_|V|), and Q(x) = (Q(x₁), …, Q(x_|V|)) is a function that maps all vertexes of ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$. Therefore, in the presence of (44), the relation

$${\mathscr{C}}({{\rm{RQNN}}}_{QG})={\mathscr{D}}({{\rm{RQNN}}}_{QG}),$$

(45)

follows for an RQNN_QG, where ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$ is the diffusion machine of RQNN_QG. It is because a constraint machine ${\mathscr{C}}({{\rm{RQNN}}}_{QG})$ that satisfies (44) is, in fact, a diffusion machine ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$, see also (41).

In (42), the f_T(RQNN_QG) state transition function can be defined for a ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$ via constraint (42) as

$${f}_{T}({{\rm{RQNN}}}_{QG})=|{\gamma }_{v}\rangle .$$

(46)

Then, let H_t be a unit vector for a unitary U_t(θ_t), t = 1, …, L − 1, defined as

$${H}_{t}={x}_{t}+i{y}_{t},$$

(47)

where x_t and y_t are real values.

Then, let Z_t+1 be defined via $U(\overrightarrow{\theta })$ and (47) as

$${Z}_{t+1}=U(\overrightarrow{\theta }){H}_{t}+E{x}_{t+1},$$

(48)

where E is a basis vector matrix⁶⁰.

Then, by rewriting $U(\overrightarrow{\theta })$ as

$$U(\overrightarrow{\theta })=\varphi +i\phi ,$$

(49)

where ϕ, φ are real parameters, allows us to evaluate $U(\overrightarrow{\theta }){H}_{t}$ as

$$(\begin{array}{l}{\rm{Re}}(U(\overrightarrow{\theta }){H}_{t})\\ {\rm{Im}}(U(\overrightarrow{\theta }){H}_{t}\end{array})=(\begin{array}{ll}\varphi & -\phi \\ \phi & \varphi \end{array})(\begin{array}{l}{x}_{t}\\ {y}_{t}\end{array})$$

(50)

with

$${H}_{t+1}={f}_{\sigma }^{{{\rm{RQNN}}}_{QG}}({Z}_{t+1}),$$

(51)

where H_t+1 is normalized at unity, and function ${f}_{\sigma }^{{{\rm{RQNN}}}_{QG}}(\cdot )$ is defined as

$${f}_{\sigma }^{{{\rm{RQNN}}}_{QG}}(Z)=\{\begin{array}{ll}Z, & {\rm{if}}\,{|Z|}_{1}\ge 0\\ \mathrm{0,} & {\rm{if}}\,{|Z|}_{1} < 0\end{array},$$

(52)

where |⋅|₁ is the L1-norm.

Since the RQNN_QG has linear transition function, (52) is also linear, and allows us to rewrite (52) via the environmental graph representation for a particular (γ_Γ(v), x_v), as

$${f}_{\sigma }^{{{\rm{RQNN}}}_{QG}}(Z)=\{\begin{array}{ll}{f}_{T}({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v}), & {\rm{if}}\,{|Z|}_{1}\ge 0\\ \mathrm{0,} & {\rm{if}}\,{|Z|}_{1} < 0\end{array},$$

(53)

where f_T(γ_Γ(v), x_v) is given in (50).

Thus, by setting t = ν, the term H_t can be rewritten via (50) and (52) as

$${H}_{t}={x}_{\nu }={\rm{Re}}({x}_{\nu })+i\,{\rm{Im}}({x}_{\nu }).$$

(54)

Then, the Y_t(RQNN_QG) output of RQNN_QG is evaluated as

$${Y}_{t}({{\rm{RQNN}}}_{QG})=W(\begin{array}{l}{\rm{Re}}({x}_{\nu })\\ {\rm{Im}}({x}_{\nu })\end{array}),$$

(55)

where W is an output matrix⁶⁰.

Then let |Γ(v)| = L, therefore at a particular objective function f(θ) of the RQNN_QG, the derivative $\frac{df(\theta )}{d{x}_{\nu }}$ can be evaluated as

$$\begin{array}{rcl}\frac{df(\theta )}{d{x}_{\nu }} & = & \frac{df(\theta )}{d{x}_{|{\rm{\Gamma }}(v)|}}\frac{d{x}_{|{\rm{\Gamma }}(v)|}}{d{x}_{\nu }}\\ & = & \frac{df(\theta )}{d{x}_{|{\rm{\Gamma }}(v)|}}\mathop{\prod }\limits_{k=\nu }^{|{\rm{\Gamma }}(v)|-1}\frac{d{x}_{k+1}}{d{x}_{k}}\\ & = & \frac{df(\theta )}{d{x}_{|{\rm{\Gamma }}(v)|}}\mathop{\prod }\limits_{k=\nu }^{|{\rm{\Gamma }}(v)|-1}{D}_{k+1}{(U(\overrightarrow{\theta }))}^{T},\end{array}$$

(56)

where

$${D}_{k+1}=diag({Z}_{k+1})$$

(57)

is a Jacobian matrix⁶⁰. For the norms the relation

$$\Vert \frac{df(\theta )}{d{x}_{\nu }}\Vert \le \Vert \frac{df(\theta )}{d{x}_{|{\rm{\Gamma }}(v)|}}\Vert \mathop{\prod }\limits_{k=\nu }^{|{\rm{\Gamma }}(v)|-1}\Vert {D}_{k+1}{(U(\overrightarrow{\theta }))}^{T}\Vert ,$$

(58)

holds, where

$$\Vert {D}_{k+1}{(U(\overrightarrow{\theta }))}^{T}\Vert =\Vert {D}_{k+1}\Vert .$$

(59)

The proof is concluded here.■

Optimal Learning

Gate-model quantum neural network

Theorem 3

A supervised learning is an optimal learning for a ${\mathscr{C}}({{\rm{QNN}}}_{QG})$.

Proof. Let π_v be the compact constraint on f_T(QNN_QG) and F_O(QNN_QG) of ${\mathscr{C}}({{\rm{QNN}}}_{QG})$ from (38), and let A be a constraint matrix. Then, (38) can be reformulated as

$${\pi }_{v}({f}_{T}({{\rm{QNN}}}_{QG}),{F}_{O}({{\rm{QNN}}}_{QG}))=A{f}^{\ast }(x)-b(x)=0.$$

(60)

where b(x) is a smooth vector-valued function with compact support⁴⁸, ${f}^{\ast }: {\mathcal I} \to {{\mathbb{C}}}^{n}$,

$${f}^{\ast }(x)=({f}_{T}({{\rm{QNN}}}_{QG}),{F}_{O}({{\rm{QNN}}}_{QG}),x)$$

(61)

is the compact function subject to be determined such that

$$\forall x\in {\mathscr{X}}:{\pi }_{v}(v,{f}^{\ast }(x))=0.$$

(62)

The problem formulated via (60) can be rewritten as

$$A{f}^{\ast }(x)=b(x).$$

(63)

As follows, learning of functions f_T(QNN_QG) and F_O(QNN_QG) of ${\mathscr{C}}({{\rm{QNN}}}_{QG})$ can be reduced to the determination of function f^*(x), which problem is solvable via the Euler-Lagrange equations^48,63,64.

Then, let ${{\mathscr{S}}}_{L({\rm{QNN}})}$ be a non-empty supervised learning set defined as a collection

$${{\mathscr{S}}}_{L({\rm{QNN}})}:\{{x}_{\kappa },{y}_{\kappa },\kappa \in {{\mathbb{N}}}_{{\mathscr{X}}}\},$$

(64)

where (x_κ, y_κ), y_κ = f^*(x_κ) is a supervised pair, and $|{\mathscr{X}}|$ is the cardinality of the perceptive space ${\mathscr{X}}$ associated with ${{\mathscr{S}}}_{L({\rm{QNN}})}$.

Since ${{\mathscr{S}}}_{L({\rm{QNN}})}$ is non-empty set, f^*(x) can be evaluated by the Euler-Lagrange equations^48,63,64, as

$${f}^{\ast }(x)=\frac{1}{\ell }(-{A}^{T}\lambda (x)-\frac{1}{|{\mathscr{X}}|}\mathop{\sum }\limits_{\kappa =1}^{|{\mathscr{X}}|}({f}^{\ast }(x)-{y}_{\kappa })\Upsilon (x-{x}_{\kappa })),$$

(65)

where A^T is the transpose of the constraint matrix A, and $\ell$ is a differential operator as

$$\ell =\mathop{\sum }\limits_{\kappa =0}^{k}{(-1)}^{\kappa }{c}_{\kappa }{\nabla }^{2\kappa },$$

(66)

where c_κ-s are constants, ${\nabla }^{2}$ is a Laplacian operator such that ${\nabla }^{2}f(x)={\sum }_{i}{\partial }_{i}^{2}f(x)$; while Υ is as

$$\Upsilon (x-{x}_{\kappa })=\ell {\mathscr{G}}(x,{x}_{\kappa }),$$

(67)

where ${\mathscr{G}}(\cdot )$ is the Green function of differential operator $\ell$. Since function ${\mathscr{G}}(\,\cdot \,)$ is translation invariant, the relation

$${\mathscr{G}}(x,{x}_{\kappa })={\mathscr{G}}(x-{x}_{\kappa })$$

(68)

follows. Since the constraint that has to be satisfied over the perceptual space ${\mathscr{X}}$ is given in (62), the ${\mathcal L}$ Lagrangian can be defined as

$$ {\mathcal L} =\langle P{f}^{\ast },P{f}^{\ast }\rangle +{\int }_{{\mathscr{X}}}\lambda (x){\pi }_{v}(x,{f}^{\ast }(x))dx,$$

(69)

where 〈⋅,⋅〉 is the inner product operator, while P is defined via (66) as

$$\ell ={P}^{\dagger }P,$$

(70)

where ${P}^{\dagger }$ is the adjoint of P, while λ(x) is the Lagrange multiplier as

$$\lambda (x)=-{(A{A}^{T})}^{-1}(\gamma \ell b(x)+\frac{1}{{\mathscr{X}}}\mathop{\sum }\limits_{\kappa =1}^{|{\mathscr{X}}|}A({f}^{\ast }(x)-{y}_{\kappa })\Upsilon (x-{x}_{\kappa })),$$

(71)

where

$$\gamma ={\int }_{{\mathscr{X}}}{\mathscr{G}}(x-{x}_{\kappa }),$$

(72)

and $\ell b$ is as

$$\ell b(x)=-A({A}^{T}\lambda (x)+\frac{1}{|{\mathscr{X}}|}\mathop{\sum }\limits_{\kappa =1}^{|{\mathscr{X}}|}({f}^{\ast }(x)-{y}_{\kappa })\Upsilon (x-{x}_{\kappa })).$$

(73)

Then, (65) can be rewritten using (71) and (73) as

$${f}^{\ast }(x)=\frac{1}{\gamma \ell }(H(x)+\frac{1}{|{\mathscr{X}}|}\mathop{\sum }\limits_{\kappa =1}^{|{\mathscr{X}}|}{\rm{\Phi }}({y}_{\kappa }-{f}^{\ast }(x))\Upsilon (x-{x}_{\kappa })),$$

(74)

where H(x) is as

$$H(x)=\gamma {A}^{T}{(A{A}^{T})}^{-1}\ell b(x)$$

(75)

and Φ is as

$${\rm{\Phi }}={{\bf{I}}}_{n}-{A}^{T}{(A{A}^{T})}^{-1}A,$$

(76)

where I_n is an identity matrix.

Therefore, after some calculations, f^*(x) can be expressed as

$${f}^{\ast }(x)=\frac{1}{\gamma }{\int }_{{\mathscr{X}}}{\mathscr{G}}(z)H(x-z)dz+\mathop{\sum }\limits_{\kappa =1}^{|{\mathscr{X}}|}{\rm{\Phi }}{\chi }_{\kappa }{\mathscr{G}}(x-{x}_{\kappa }),$$

(77)

where χ_κ is as

$${\chi }_{\kappa }=\frac{1}{|{\mathscr{X}}|}\frac{{y}_{\kappa }-{f}^{\ast }({x}_{\kappa })}{\gamma }.$$

(78)

The compact constraint of ${\mathscr{C}}({{\rm{QNN}}}_{QG})$ determined via (77) is optimal, since (77) is the optimal solution of the Euler–Lagrange equations.

The proof is concluded here.■

Lemma 1

There exists a supervised learning for a ${\mathscr{C}}({{\rm{QNN}}}_{QG})$ with complexity ${\mathscr{O}}(|S|)$, where |S| is the number arcs (number of gate parameters) of ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$.

Proof. Let ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$ be the environmental graph of QNN_QG, such that QNN_QG is characterized via $\overrightarrow{\theta }$ (see (3)).

The optimal supervised learning method of a ${\mathscr{C}}({{\rm{QNN}}}_{QG})$ is derived through the utilization of the ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$ environmental graph of QNN_QG, as follows.

The ${{\mathscr{A}}}_{{\mathscr{C}}({{\rm{QNN}}}_{QG})}$ learning process of ${\mathscr{C}}({{\rm{QNN}}}_{QG})$ in the ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$ structure is given in Algorithm 1.

The optimality of Algorithm 1 arises from the fact that in Step 4, the gradient computation involves all the gate parameters of the QNN_QG, and the gate parameter updating procedure has a computational complexity ${\mathscr{O}}(|S|)$. The QNN_QG complexity is yielded from the gate parameter updating mechanism that utilizes backpropagated classical side information for the learning method.

The proof is concluded here.■

Algorithm 1

Superviseid learning for a ${\mathscr{C}}({{\rm{QNN}}}_{QG})$.

Description and method validation

The detailed steps and validation of Algorithm 1 are as follows.

In Step 1, the number R of measurement rounds is set.

Step 2 is the quantum evolution phase of QNN_QG that yields an output quantum system $|Y\rangle$ via forward propagation of quantum information through the unitary sequence $U(\overrightarrow{\theta })$ realized via the L unitaries. Then, a parameterization follows for each ${x}_{{U}_{i}({\theta }_{i})}$, and the terms ${W}_{{U}_{i}({\theta }_{i})}$ and ${Q}_{{U}_{i}({\theta }_{i})}$ are defined to characterize the θ_i angles of the U_i(θ_i) unitary operations in the QNN_QG.

In Step 3, side information initializations are made for the error computations. A given ${W}_{{U}_{i}({\theta }_{i})}$ is set as a cumulative quantity with respect to the parent set Ξ ∈ i of unitary U_i(θ_i) in QNN_QG.

Note, that (80) and (81) represent side information, thus the gate parameter θ_hi is used to identify a particular unitary U(θ_hi).

Let ${{\mathscr{G}}^{\prime} }_{{{\rm{QNN}}}_{QG}}$ be the the environmental graph of QNN_QG such that the directions of quantum links are reversed. It can be verified that for a ${{\mathscr{G}}^{\prime} }_{{{\rm{QNN}}}_{QG}}$, ${\delta }_{{U}_{i}({\theta }_{i})}$ from (82) can be rewritten as

$${\delta }_{{U}_{i}({\theta }_{i})}=\sum _{h\in \Xi (i)}\frac{d{W}_{{U}_{L}({\theta }_{L})}}{d{Q}_{{U}_{h}({\theta }_{h})}}\frac{d{Q}_{{U}_{h}({\theta }_{h})}}{d{W}_{{U}_{i}({\theta }_{i})}}\frac{d{W}_{{U}_{i}({\theta }_{i})}}{d{Q}_{{U}_{i}({\theta }_{i})}}={Q}_{{U}_{i}({\theta }_{i})}\sum _{h\in \Xi (i)}{\theta }_{hi}{\delta }_{{U}_{h}({\theta }_{h})},$$

(89)

and ${\delta }_{{U}_{L}({\theta }_{L})}$ can be evaluated as given in (83)

$${\delta }_{{U}_{L}({\theta }_{L})}=\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{Q}_{{U}_{L}({\theta }_{L})}},$$

(90)

while the term ${\delta }_{{U}_{i}({\theta }_{i})}{W}_{{U}_{j}({\theta }_{j})}$ for each U_i(θ_i) can be rewritten as

$${\delta }_{{U}_{i}({\theta }_{i})}{W}_{{U}_{j}({\theta }_{j})}=\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{\theta }_{ij}}=\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{Q}_{{U}_{i}({\theta }_{i})}}\frac{d{Q}_{{U}_{i}({\theta }_{i})}}{d{\theta }_{ij}}\mathrm{.}$$

(91)

Since (86) and (85) are defined via the non-reversed ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$, for a given unitary the Γ children set is used. The utilization of the Ξ parent set with reversed link directions in ${{\mathscr{G}}^{\prime} }_{{{\rm{QNN}}}_{QG}}$ (see (89), (90), (91)) is therefore analogous to the use of the Γ children set with non-reversed link directions in ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$. It is because classical side information is available in arbitrary directions in ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$.

First, we consider the situation, if i = 1, …, L − 1, thus the error calculations are associated to unitaries U₁(θ₁), …, U_L−1(θ_L−1), while the output unitary U_L(θ_L) is proposed for the i = L case.

In ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$, the error quantity ${\delta }_{{U}_{i}({\theta }_{i})}$ associated to U_i(θ_i) is determined, where ${W}_{{U}_{L}({\theta }_{L})}$ is associated to the output unitary U_L(θ_L). Only forward steps are required to yield ${W}_{{U}_{L}({\theta }_{L})}$ and ${Q}_{{U}_{L}({\theta }_{L})}$. Then, utilizing the chain rule and using the children set Γ(i) of a particular unitary U_i(θ_i), the term $d{W}_{{U}_{L}({\theta }_{L})}/d{Q}_{{U}_{i}({\theta }_{i})}$ in ${\delta }_{{U}_{i}({\theta }_{i})}$ can be rewritten as $\frac{d{W}_{{U}_{L}({\theta }_{L})}}{d{Q}_{{U}_{i}({\theta }_{i})}}={\sum }_{h\in {\rm{\Gamma }}(i)}\frac{d{W}_{{U}_{L}({\theta }_{L})}}{d{Q}_{{U}_{h}({\theta }_{h})}}\frac{d{Q}_{{U}_{h}({\theta }_{h})}}{d{W}_{{U}_{i}({\theta }_{i})}}\frac{d{W}_{{U}_{i}({\theta }_{i})}}{d{Q}_{{U}_{i}({\theta }_{i})}}$. In fact, this term equals to ${Q}_{{U}_{i}({\theta }_{i})}{\sum }_{h\in {\rm{\Gamma }}(i)}{\theta }_{hi}{\delta }_{{U}_{h}({\theta }_{h})}$, where ${\delta }_{{U}_{h}({\theta }_{h})}$ is the error associated to a U_h(θ_h), such that U_h(θ_h) is a children unitary of U_i(θ_i). The ${\delta }_{{U}_{h}({\theta }_{h})}$ error quantity associated to a children unitary U_h(θ_h) of U_i(θ_i) can also be determined in the same manner, that yields ${\delta }_{{U}_{h}({\theta }_{h})}=d{W}_{{U}_{L}({\theta }_{L})}/d{Q}_{{U}_{h}({\theta }_{h})}$. As follows, by utilizing side information in ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$ allows us to determine ${\delta }_{{U}_{i}({\theta }_{i})}$ via the ${\mathcal L} (\,\cdot \,)$ loss function and the Γ(i) children set of unitary U_i(θ_i), that yields the quantity given in (82).

The situation differs if the error computations are made with respect to the output system, thus for the L-th unitary U_L(θ_L). In this case, the utilization of the loss function ${\mathcal L} ({x}_{0},\tilde{l}(z))$ allows us to use the simplified formula of ${\delta }_{{U}_{L}({\theta }_{L})}=d {\mathcal L} ({x}_{0},\tilde{l}(z))/d{Q}_{{U}_{L}({\theta }_{L})}$, as given in (83). Taking the $\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{\theta }_{ij}}$ derivative of the loss function ${\mathcal L} ({x}_{0},\tilde{l}(z))$ with respect to the angle θ_ij yields $\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{Q}_{{U}_{i}({\theta }_{i})}}\frac{d{Q}_{{U}_{i}({\theta }_{i})}}{d{\theta }_{ij}}$, that is, in fact equals to ${\delta }_{{U}_{i}({\theta }_{i})}{W}_{{U}_{j}({\theta }_{j})}$.

In Step 4, the quantities defined in the previous steps are utilized in the QNN_QG for the error calculations. The errors are evaluated and updated in a backpropagated manner from unitary U_L(θ_L) to U₁(θ₁). Since it requires only side information these steps can be achieved via a ${\rm{P}}({{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}})$ post-processing (along with Step 3). First, a gate parameter modification vector $\overrightarrow{{\rm{\Delta }}}\theta$ is defined, such that its i-th element, $\overrightarrow{{\rm{\Delta }}}{\theta }_{i}$, is associated with the modification of the θ_i gate parameter of an i-th unitary U_i(θ_i).

The i-th element $\overrightarrow{{\rm{\Delta }}}{\theta }_{i}$ is initialized as $\overrightarrow{{\rm{\Delta }}}{\theta }_{i}={W}_{{U}_{i}({\theta }_{i})}$. If $\overrightarrow{{\rm{\Delta }}}{\theta }_{i}$ equals to 1, then no modification is required in the θ_i gate parameter of U_i(θ_i). In this case, the ${\delta }_{{U}_{i}({\theta }_{i})}$ error quantity of U_i(θ_i) can be determined via a simple summation, using the children set of U_i(θ_i), as ${\delta }_{{U}_{i}({\theta }_{i})}={\sum }_{j\in {\rm{\Gamma }}(i)}{\theta ^{\prime} }_{ij}{\delta }_{{U}_{j}({\theta }_{j})}$, where U_j(θ_j) is a children of U_i(θ_i), as it is given in (85). On the other hand, if $\overrightarrow{{\rm{\Delta }}}{\theta }_{i}\ne 1$, then the θ_i gate parameter of U_i(θ_i) requires a modification. In this case, summation ${\sum }_{j\in \Gamma (i)}{\theta }_{ij}{\delta }_{{U}_{j}({\theta }_{j})}$ has to be weighted by the actual $\overrightarrow{{\rm{\Delta }}}{\theta }_{i}$ to yield ${\delta }_{{U}_{i}({\theta }_{i})}$. This situation is obtained in (86).

According to the update mechanism of (84–86), for z = L − 1, …, 1, the errors are updated via (88) as follows. At z = L and $\overrightarrow{{\rm{\Delta }}}{\theta }_{z}=1$, ${\delta }_{{U}_{z}({\theta }_{z})}$ is as

$${\delta ^{\prime} }_{{U}_{z}({\theta }_{z})}={\delta }_{{U}_{L}({\theta }_{L})}\mathrm{.}$$

(92)

while at $\overrightarrow{{\rm{\Delta }}}{\theta }_{z}\ne 1$, ${\delta }_{{U}_{z}({\theta }_{z})}$ is updated as

$${\delta ^{\prime} }_{{U}_{z}({\theta }_{z})}=(\overrightarrow{{\rm{\Delta }}}{\theta }_{z}){\delta }_{{U}_{L}({\theta }_{L})}.$$

(93)

For z = L − 1, …, 1, if $\overrightarrow{{\rm{\Delta }}}{\theta }_{z}=1$, then ${\delta }_{{U}_{z}({\theta }_{z})}$ is as

$${\delta ^{\prime} }_{{U}_{z}({\theta }_{z})}={\delta }_{{U}_{z}({\theta }_{z})}=\sum _{j\in \Gamma (z)}{\theta }_{zj}{\delta }_{{U}_{j}({\theta }_{j})}\mathrm{.}$$

(94)

while, if $\overrightarrow{{\rm{\Delta }}}{\theta }_{z}\ne 1$, then

$${\delta ^{\prime} }_{{U}_{z}({\theta }_{z})}=(\overrightarrow{\Delta }{\theta }_{z})\sum _{j\in {\rm{\Gamma }}(z)}{\theta }_{zj}{\delta }_{{U}_{j}({\theta }_{j})}=\sum _{j\in {\rm{\Gamma }}(z)}{\theta ^{\prime} }_{zj}{\delta }_{{U}_{j}({\theta }_{j})}.$$

(95)

In Step 5, for a given unitary U_i(θ_i), i = 2, …, L and for its parent U_j(θ_j), the ${g}_{{U}_{i}({\theta }_{i}),{U}_{j}({\theta }_{j})}$ gradient is computed via the ${\delta }_{{U}_{i}({\theta }_{i})}$ error quantity derived from (85–86) for U_i(θ_i), and by the ${W}_{{U}_{j}({\theta }_{j})}$ quantity associated to parent U_j(θ_j). (For U₁(θ₁) the parent set Ξ(1) is empty, thus i > 1.) The computation of ${g}_{{U}_{i}({\theta }_{i}),{U}_{j}({\theta }_{j})}$ is performed for all U_j(θ_j) parents of U_i(θ_i), thus (87) is determined for ∀j, j ∈ Ξ(i). By the chain rule,

$$\begin{array}{rcl}{g}_{{U}_{i}({\theta }_{i}),{U}_{j}({\theta }_{j})}={\delta ^{\prime} }_{{U}_{i}({\theta }_{i})}{W}_{{U}_{j}({\theta }_{j})} & = & \frac{d{W}_{{U}_{L}({\theta }_{L})}}{d{\theta ^{\prime} }_{ij}}\\ & = & \frac{d{W}_{{U}_{L}({\theta }_{L})}}{d{Q}_{{U}_{i}({\theta }_{i})}}\frac{d{Q}_{{U}_{i}({\theta }_{i})}}{d{\theta ^{\prime} }_{ij}}\\ & = & \frac{d{W}_{{U}_{L}({\theta }_{L})}}{d{Q}_{{U}_{i}({\theta }_{i})}}\frac{d(\sum _{h\in {\rm{\Xi }}(i)}{\theta }_{hi}{W}_{{U}_{h}({\theta }_{h})})}{d{\theta ^{\prime} }_{ij}}.\end{array}$$

(96)

Since for i = L, ${\delta }_{{U}_{L}({\theta }_{L})}$ is as given in (83), the gradient can be rewritten via (91) as

$$\begin{array}{l}{g}_{{U}_{i}({\theta }_{i}),{U}_{j}({\theta }_{j})}=\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{\theta ^{\prime} }_{ij}}\end{array}.$$

(97)

Finally, Step 6 utilizes the number R of measurements to extend the results for all measurement rounds, r = 1, …, R. Note that in each round a measurement operator is applied, for simplicity it is omitted from the description.

Since the algorithm requires no reversed quantum links, i.e. ${{\mathscr{G}}^{\prime} }_{{{\rm{QNN}}}_{QG}}$ for the computations of (85–86), the gradient of the loss in (87) with respect to the gate parameter can be determined in an optimal way for QNN_QG networks, by the utilization of side information in ${{\mathscr{G}}}_{{{\rm{QNN}}}_{QG}}$.

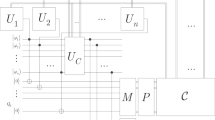
The steps and quantities of the learning procedure (Algorithm 1) of a QNN_QG are illustrated in Fig. 3. The QNN_QG network realizes the unitary $U(\overrightarrow{\theta })$. The quantum information is propagated through quantum links (solid lines) between the unitaries, while the auxiliary classical information is propagated via classical links in the network (dashed lines). An i-th node is represented via unitary U_i(θ_i).

Figure 3

The learning method for a QNN_QG. The QNN_QG network realizes unitary $U(\overrightarrow{\theta })$ as a sequence of L unitaries, $U(\overrightarrow{\theta })={U}_{L}({\theta }_{L}){U}_{L-1}({\theta }_{L-1})\ldots {U}_{1}({\theta }_{1})$. The algorithm determines the gradient of the loss with respect to the θ gate parameter, at a particular loss function ${\mathcal L} ({x}_{0},\tilde{l}(z))$. All quantum information propagates forward via quantum links (solid lines), classical side information can propagate arbitrarily (dashed lines).

For an i-th unitary, U_i(θ_i), parameters ${W}_{{U}_{i}({\theta }_{i})}$, ${Q}_{{U}_{i}({\theta }_{i})}$ and ${\delta }_{{U}_{i}({\theta }_{i})}=d{W}_{{U}_{L}({\theta }_{L})}/d{Q}_{{U}_{i}({\theta }_{i})}$ for i < L, are computed, where ${W}_{{U}_{L}({\theta }_{L})}={\sum }_{j\in \Xi (L)}{\theta }_{Lj}{V}_{{U}_{j}({\theta }_{j})}$. For the output unitary, ${\delta }_{{U}_{L}({\theta }_{L})}=d {\mathcal L} ({x}_{0},\tilde{l}(z))/d{Q}_{{U}_{L}({\theta }_{L})}$. Parameters ${W}_{{U}_{i}({\theta }_{i})}$ and ${Q}_{{U}_{i}({\theta }_{i})}$ are determined via forward propagation of side information, the ${\delta }_{{U}_{i}({\theta }_{i})}$ quantities are evaluated via backward propagation of side information. Finally, the gradients, ${g}_{{U}_{i}({\theta }_{i}),{U}_{j}({\theta }_{j})}={\delta }_{{U}_{i}({\theta }_{i})}{W}_{{U}_{j}({\theta }_{j})},$ are computed.

Recurrent gate-model quantum neural network

In classical neural networks, backpropagation^59,60,61 (backward propagation of errors) is a supervised learning method that allows to determine the gradients to learn the weights in the network. In this section, we show that for a recurrent gate-model QNN, a backpropagation method is optimal.

Theorem 4

A backpropagation in ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ is an optimal learning in the sense of gradient descent.

Proof. In an RQNN_QG, the backward classical links provide feedback side information for the forward propagation of quantum information in multiple measurement rounds. The backpropagated side information is analogous to feedback loops, i.e, to recurrent cycles over time. The aim of the learning method is to optimize the gate parameters of the unitaries of the RQNN_QG quantum network via a supervised learning, using the side information available from the previous k = 1, …, r − 1 measurement rounds at a particular measurement round r.

Let ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ be the environmental graph of RQNN_QG, and f_T(RQNN_QG) be the transition function of an RQNN_QG. Then the γ_v constraint is defined via ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ as

$$|{\gamma }_{v}\rangle ={f}_{T}({{\rm{RQNN}}}_{QG})={f}_{T}({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v}),$$

(98)

while the constraint Ω_v on the output F(γ_v, x_v) of RQNN_QG is defined via ω_v = 0 as^48,61,62

$${\omega }_{v}:{{\rm{\Omega }}}_{v}F({f}_{T}({{\rm{RQNN}}}_{QG}),{x}_{v})={{\rm{\Omega }}}_{v}\circ F({f}_{T}({\gamma }_{{\rm{\Gamma }}(v)},{x}_{v}),{x}_{v})=0.$$

(99)

Utilizing the structure of the ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ environmental graph allows us to define a modified version of the backpropagation through time algorithm⁵⁹ to the RQNN_QG.

The learning of ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$ with constraints (42), (43), and (44) is given in Algorithm 2, depicted as ${{\mathscr{A}}}_{{\mathscr{D}}({{\rm{RQNN}}}_{QG})}$.

As a corollary, the training of ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$ can be reduced to a backpropagation method via the environmental graph of RQNN_QG.■

Algorithm 2

Optimal learning method for a ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$.

Description and method validation

The detailed steps and validation of Algorithm 2 are as follows.

In Step 1, the number R of measurement rounds are set for RQNN_QG. For each measurement round initialization steps (100, 101) are set.

Step 2 provides the quantum evolution phase of RQNN_QG, and produces output quantum system $|{Y}_{r}\rangle$ (102) via forward propagation of quantum information through the unitary sequence $U({\overrightarrow{\theta }}_{r})$ of the L unitaries.

Step 3 initializes the P^(r)(RQNN_QG) post-processing method via the definition of (105) for gradient computations. In (106), the quantity ${{\rm{\Phi }}}_{r}={z}^{(r)}+U({\overrightarrow{\theta }}_{r-1})+{B}_{r}$ connects the side information of the r-th measurement round with the side information of the (r − 1)-th measurement round; and $U({\overrightarrow{\theta }}_{r-1})$ is the unitary sequence of the (r − 1)-th round, and B_r is a bias the current measurement round. The quantity ξ_r,k = dΦ_r/dΦ_k in (107) utilizes the Φ_i quantities (see (106)) of the i-th measurement rounds, such that i = k + 1, …, r, where k < r.

Step 4 determines the g_r loss function gradient of the r-th measurement round. In (108), the g_r gradient is determined as ${\sum }_{k=1}^{r}\frac{ {\mathcal L} ({x}_{\mathrm{0,}r},\tilde{l}({z}^{(r)}))}{d{{\rm{\Phi }}}_{r}}\frac{d{{\rm{\Phi }}}_{r}}{d{{\rm{\Phi }}}_{k}}\frac{d{\tilde{{\rm{\Phi }}}}_{k}}{d{\mathscr{S}}({\overrightarrow{\theta }}_{r})}$, that is, via the utilization of the side information of the k = 1, …, r measurement rounds at a particular r.

In Step 5, the gate parameters are updated via the gradient descent rule⁵⁹ by utilizing the gradients of the k = 1, …, r measurement rounds at a particular r. Since in (111) all the gate parameters of the L unitaries are updated by ω_r as given in (112), for a particular unitary U_i(θ_r,i), the gate parameter is updated via ${\overrightarrow{\alpha }}_{r}$ (114) to θ_r+1,i as

$${\theta }_{r+\mathrm{1,}i}={\theta }_{r,i}-{\alpha }_{r,i}={\theta }_{r,i}-{\omega }_{r}\mathrm{.}$$

(117)

Finally, Step 6 outputs the G final gradient of the total R measurement rounds in (116), as a summation of the g_r gradients (108) determined in the r = 1, …, R rounds.

The steps of the learning method of an RQNN_QG (Algorithm 2) are illustrated in Fig. 4. The ${\overrightarrow{\theta }}_{r}$ gate parameters of the unitaries of unitary sequence $U({\overrightarrow{\theta }}_{r})$ are set as ${\overrightarrow{\theta }}_{r}={\overrightarrow{\theta }}_{r-1}-{\omega }_{r-1},$ where ${\overrightarrow{\theta }}_{r-1}$ is the gate parameter vector associated to sequence $U({\overrightarrow{\theta }}_{r-1})$, while α_r−1,i = ω_r−1 is the gate parameter modification coefficient, and ${\omega }_{r-1}=\frac{\lambda }{r-1}{\sum }_{k=1}^{r-1}\frac{ {\mathcal L} ({x}_{\mathrm{0,}k},\tilde{l}({z}^{(k)}))}{d{\mathscr{S}}({\overrightarrow{\theta }}_{k})}$.

Figure 4

The learning method for an RQNN_QG. In an r-th measurement round, the RQNN_QG network realizes the unitary sequence $U({\overrightarrow{\theta }}_{r})$, and side information is available about the previous k = 1, …, r − 1 running sequences of the structure. Quantum information propagates only forward in the network via quantum links (solid lines), the α_r−1,i = ω_r−1 quantities are distributed via backpropagation of side information through the classical links (dashed lines). The θ_r,j gate parameter of an i-th unitary U_i(θ_r,i) of $U({\overrightarrow{\theta }}_{r})$ is set to θ_r,i = θ_r−1,i − α_r−1,i, where θ_r−1,i is the gate parameter of the i-th unitary U_i(θ_r−1,i) of the $U({\overrightarrow{\theta }}_{r-1})$ unitary sequence.

Closed-form error evaluation

Lemma 2

The δ quantity of the unitaries of a ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$ can be expressed in a closed form via the ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ environmental graph of RQNN_QG.

Proof. Let ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ be the environmental graph of RQNN_QG, such that RQNN_QG is characterized via $\overrightarrow{\theta }$ (see (3)). Utilizing the structure ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ of RQNN_QG allows us to express the square error in a closed form as follows.

Let Y and Z refer to output realizations $|Y\rangle$ and $|Z\rangle$ of RQNN_QG, ${\mathscr{Y}}\in Y,Z$, with an output set ${\mathscr{Y}}$, and let ${\mathcal L} ({x}_{0},\tilde{l}(z))$ be the loss function. Then let ${{\bf{H}}}_{{{\rm{RQNN}}}_{QG}}$ be a Hessian matrix⁴⁸ of the RQNN_QG structure, with a generic coordinate ${\hslash }_{ij,lm}^{{{\rm{RQNN}}}_{QG}}$, as

$$\begin{array}{rcl}{\hslash }_{ij,lm}^{{{\rm{RQNN}}}_{QG}} & = & \frac{{d}^{2} {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{\theta }_{ij}d{\theta }_{lm}}\\ & = & \frac{d}{d{\theta }_{ij}}\sum _{Y\in {\mathscr{Y}}}\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{W}_{{U}_{Y}({\theta }_{Y})}}\frac{d{W}_{{U}_{Y}({\theta }_{Y})}}{d{\theta }_{lm}}\\ & = & \sum _{Y\in {\mathscr{Y}}}\sum _{Z\in {\mathscr{Y}}}\frac{{d}^{2} {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{W}_{{U}_{Y}({\theta }_{Y})}d{W}_{{U}_{Z}({\theta }_{Z})}}{\delta }_{{U}_{i}({\theta }_{i})}^{Z}{\delta }_{{U}_{l}({\theta }_{l})}^{Y}{W}_{{U}_{j}({\theta }_{j})}{W}_{{U}_{m}({\theta }_{m})}\\ & & +\sum _{Y\in {\mathscr{Y}}}\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{W}_{{U}_{Y}({\theta }_{Y})}}({W}_{{U}_{m}({\theta }_{m})}\frac{d{\delta }_{{U}_{l}({\theta }_{l})}^{Y}}{d{\theta }_{ij}}+{\delta }_{{U}_{l}({\theta }_{l})}^{Y}\frac{d{W}_{{U}_{m}({\theta }_{m})}}{d{\theta }_{ij}})\\ & = & \sum _{Y\in {\mathscr{Y}}}\sum _{Z\in {\mathscr{Y}}}\frac{{d}^{2} {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{W}_{{U}_{Y}({\theta }_{Y})}d{W}_{{U}_{Z}({\theta }_{Z})}}{\delta }_{{U}_{i}({\theta }_{i})}^{Z}{\delta }_{{U}_{l}({\theta }_{l})}^{Y}{W}_{{U}_{j}({\theta }_{j})}{W}_{{U}_{m}({\theta }_{m})}\\ & & +\sum _{Y\in {\mathscr{Y}}}\frac{d {\mathcal L} ({x}_{0},\tilde{l}(z))}{d{W}_{{U}_{Y}({\theta }_{Y})}}({({\delta }_{{U}_{l}({\theta }_{l}),{U}_{i}({\theta }_{i})}^{Y})}^{2}{W}_{{U}_{m}({\theta }_{m})}{W}_{{U}_{j}({\theta }_{j})}+{f}_{i\angle m}({\delta }_{{U}_{l}({\theta }_{l})}^{Y}{\delta }_{{U}_{i}({\theta }_{i})}^{m}{W}_{{U}_{j}({\theta }_{j})}))\end{array},$$

(118)

where ${W}_{{U}_{i}({\theta }_{i})}$ is given in (81), f_i∠m(⋅) is a topological ordering function on ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$, indices Y and Q are associated with the output realizations $|Y\rangle$ and $|Q\rangle$, while ${({\delta }_{{U}_{l}({\theta }_{l}),{U}_{i}({\theta }_{i})}^{Q})}^{2}$ is the square error between unitaries U_l(θ_l) and U_i(θ_i) at a particular output $|Q\rangle$ as

$$\begin{array}{rcl}{({\delta }_{{U}_{l}({\theta }_{l}),{U}_{i}({\theta }_{i})}^{Q})}^{2} & = & \frac{{d}^{2}{W}_{{U}_{Y}({\theta }_{Y})}}{d{Q}_{{U}_{l}({\theta }_{l})}d{Q}_{{U}_{i}({\theta }_{i})}}=\frac{d{\delta }_{{U}_{i}({\theta }_{i})}^{Y}}{d{Q}_{{U}_{l}({\theta }_{l})}}\\ & = & \frac{d{\delta }_{{U}_{l}({\theta }_{l})}^{i}}{d{Q}_{{U}_{i}({\theta }_{i})}}\sum _{j\in {\rm{\Gamma }}(i)}{\theta }_{ji}{\delta }_{{U}_{l}({\theta }_{l})}^{Y}+{Q}_{{U}_{i}({\theta }_{i})}\sum _{j\in {\rm{\Gamma }}(i)}{\theta }_{ji}{({\delta }_{{U}_{j}({\theta }_{l}),{U}_{l}({\theta }_{l})}^{Y})}^{2},\end{array}$$

(119)

where ${Q}_{{U}_{i}({\theta }_{i})}$ is as in (80). Note that the relation ${({\delta }_{{U}_{l}({\theta }_{l}),{U}_{i}({\theta }_{i})}^{Q})}^{2}\ne 0$ in (119) holds if only there is an edge s_il between ${v}_{{U}_{i}}\in V$ and ${v}_{{U}_{l}({\theta }_{l})}\in V$ in the environmental graph ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ of RQNN_QG. Thus,

$${({\delta }_{{U}_{l}({\theta }_{l}),{U}_{i}({\theta }_{i})}^{Q})}^{2}=\{\begin{array}{ll}{({\delta }_{{U}_{l}({\theta }_{l}),{U}_{i}({\theta }_{i})}^{Q})}^{2}=\mathrm{0,} & {\rm{if}}\,{s}_{il}\notin S\\ {({\delta }_{{U}_{l}({\theta }_{l}),{U}_{i}({\theta }_{i})}^{Q})}^{2}\ne \mathrm{0,} & {\rm{if}}\,{s}_{il}\in S\end{array}.$$

(120)

Since ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$ contains all information for the computation of (119) and ${\mathscr{D}}({{\rm{RQNN}}}_{QG})$ is defined through the structure of ${{\mathscr{G}}}_{{{\rm{RQNN}}}_{QG}}$, the proof is concluded here.■

Conclusions

Gate-model QNNs allow an experimental implementation on near-term gate-model quantum computer architectures. Here we examined the problem of learning optimization of gate-model QNNs. We defined the constraint-based computational models of these quantum networks and proved the optimal learning methods. We revealed that the computational models are different for nonrecurrent and recurrent gate-model quantum networks. We proved that for nonrecurrent and recurrent gate-model QNNs, the optimal learning is a supervised learning. We showed that for a recurrent gate-model QNN, the learning can be reduced to backpropagation. The results are particularly useful for the training of QNNs on near-term quantum computers.