Effective routing design for remote entanglement generation on quantum networks

Abstract

Quantum network is a promising platform for many ground-breaking applications that lie beyond the capability of its classical counterparts. Efficient entanglement generation on quantum networks with relatively limited resources such as quantum memories is essential to fully realize the network’s capabilities, the solution to which calls for delicate network design and is currently at the primitive stage. In this study we propose an effective routing scheme to enable automatic responses for multiple requests of entanglement generation between source-terminal stations on a quantum lattice network with finite edge capacities. Multiple connection paths are exploited for each connection request while entanglement fidelity is ensured for each path by performing entanglement purification. The routing scheme is highly modularized with a flexible nature, embedding quantum operations within the algorithmic workflow, whose performance is evaluated from multiple perspectives. In particular, three algorithms are proposed and compared for the scheduling of capacity allocation on the edges of quantum network. Embodying the ideas of proportional share and progressive filling that have been well-studied in classical routing problems, we design another scheduling algorithm, the propagatory update method, which in certain aspects overrides the two algorithms based on classical heuristics in scheduling performances. The general solution scheme paves the road for effective design of efficient routing and flow control protocols on applicational quantum networks.

Introduction

Quantum networks¹ enable many applications that lie beyond the scope of classical data networks, such as quantum communication², clock synchronization³, and distributed quantum computing^4,5,6. Most of these applications require the generation of entangled pairs between far-away stations on the quantum network. Recent experiments⁷ have demonstrated deterministic entanglement between two spatially separated solid-state memories via optical photons. The distance in this physical (hardware) layer⁸ can be further increased with low-loss optical links, such as transporting photons at the tele-communication wavelength^9,10,11.

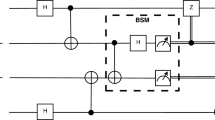
Still, the time required for remote entanglement generation increases exponentially with distance due to potential loss. In analogy with the functioning on the link layer of classical data networks, intermediate nodes on the quantum nodes could serve as quantum repeaters^{12,13,14,15,16}, by which means the exponential time cost in entanglement generation could be reduced to polynomial time scaling. Quantum repeaters (Fig. 1a) link quantum stations over longer distances by performing entanglement swapping, e.g., joint Bell state measurements at the local repeater station (see Supplemental Materials) aided by classical communication (LOCC).

Fig. 1: Routing problem statement.

a Diagram of entanglement swapping. Two remote stations can be entangled with the assistance of intermediate nodes. Black dots (lines) represent quantum memories (optical links). b Diagram of entanglement purification. With local physical operations and communication through classical channels, an entangled pair with high fidelity can be distilled from two fresh pairs with lower fidelity. c Entanglement routing on a 2D square lattice network. Edge (i, j) consists of multiple entangled pairs (multi-channels) such as Bell states, whose capacity is denoted as C_ij. Entanglement generation between S₁₍₂₎ and T₁₍₂₎ is requested and multiple paths are identified for each request. The probabilities of successfully building an entangled pair between adjacent nodes and performing local Bell state measurement are denoted as p_out and p_in, respectively.

Nevertheless, quantum repeaters sometimes might not generate entangled pairs with a certain desired fidelity, which is required in many applications using entangled pairs. For example, in quantum cryptography protocols (e.g., the BB84 protocol¹⁷), an entanglement fidelity beyond the quantum bit error rate (QBER) is required to ensure the security of key distribution. Entanglement purification is a technique that can increase the fidelity of entangled pairs, at the expense of a reduced number of entangled pairs, i.e., the purification process reduces the number of shared entangled pairs along the links between adjacent nodes on the network (Fig. 1b).

On top of the link layer mentioned above, where entanglement swapping and purifications are carried out, a network layer could be implemented for robust and well-functioning network design to enable the broader capabilities of quantum networks^18,19,20,21. In particular, the network design determines routing principles that enable effective network responses to simultaneous requests of entanglement generation between remote stations (e.g., S₁₍₂₎ − T₁₍₂₎ in Fig. 1c). Given limited quantum capacity, i.e., a small number of available quantum memories possessed by each node, it is then critical to design efficient routing protocols for simultaneous entanglement generation between multiple stations.

To tackle with this routing problem, we assume a central classical processor (scheduler) in the network which performs routing calculations and broadcasts the schedule to all network stations. Local classical processors to design the routing protocol can result in a degraded network performance²¹. At the beginning of each processing time window, upon receiving a batch of connection requests, the processor determines the paths (virtual circuits) to be initiated within the network. It then carries out the scheduling of edge capacity allocation, and determines the flow of each path according to scheduling results. Such routing information is broadcast to nodes, and local physical operations, including entanglement purification and swapping, are conducted to realize entangled connections between remote nodes. The generated entangled pairs connecting remote stations then serve as the building blocks for various quantum network applications. Entangled pairs between adjacent stations consumed in this time window are generated again to prepare for the next batch of connection requests in the consecutive time window.

Recent work by Pant et al.²¹ introduced a greedy algorithm for this routing problem on quantum lattice networks. While this algorithm works well on networks having one entangled pair shared between each pair of adjacent nodes and one connection request being processed per time window, a general routing protocol where neighboring nodes share more entangled pairs (multi-channel), and multiple user requests are simultaneously attended to (multi-request), remains an open design question. Novel architectures are to be proposed and investigated when this layer of complexity is added to the problem. Moreover, for a robust routing algorithm, it is expected that multiple paths, instead of only the shortest path, are to be utilized for each connection request, as a prevention against potential network failures.

In this study, we propose a general routing scheme which provides efficient solutions to the above entanglement generation problem, with advanced design features (multi-request, multi-path and multi-channel). We devise algorithms to effectively allocate limited quantum resources and meet the needs of entanglement generation for arbitrary connection requests, upon satisfying the fidelity threshold for generated entanglements.

Routing protocols on classical data networks have been extensively studied and are being continuously developed. Yet for quantum networks, routing schemes well-established on today’s communication networks (e.g., the Internet) are not directly applicable. The quantum no-cloning theorem forbids the duplication of entangled pairs and renders unfeasible the idea of packet switching, a major routing mechanism for large-scale data networks in which the same information package is sent multiple times along indefinite routing paths. Instead, for quantum networks, one may have to go back to early routing mechanisms that appeared when computers were expensive (note these mechanisms are still in use today for specific applications), for example, the virtual circuit switching scheme²², where one establishes temporal paths between two stations and maintains such paths during a time window, before starting over again for the next round of connection. Our routing design is based on this scheme. Conceptually, the key difference between packet switching and virtual circuit switching is the manner in which information redundancy is guaranteed, a key issue in practical routing designs in the presence of potential network failures, which are frequent and unpredictable in real applications. The no-cloning theorem decides that the redundancy of quantum information cannot be obtained through duplication of entangled pairs, while instead could be preserved in the generation of sufficient entangled pairs via virtual circuits.

The organization of the paper is as follows: we first formalize the problem statement of this study, based on which the stepwise routing scheme is introduced. Three algorithms are proposed for the scheduling of capacity allocation on network edges, in which adjacent entangled pairs are properly distributed upon connection requests. The routing performance is evaluated from multiple perspectives, and a sample routing result is demonstrated and explained in detail. We then conduct extensive simulations to discuss system parameters, compare the three scheduling algorithms, and investigate the robustness of the scheme under different conditions. Limitations, scope of usage as well as potential extensions of the current study are discussed in the end, where the paper is concluded.

Results

Problem statement

Consider a lattice quantum network G(V, E) of V nodes and E edges. Each node represents a quantum station with a finite number of qubit memories (here we assume first-generation quantum repeaters¹⁶) The edge capacity C₀ is defined as the maximal number of entangled pairs that can be generated between adjacent nodes. Without loss of generality, we consider maximally entangled states (Bell states) between adjacent nodes, $\left|{{{\Phi }}}^{\pm }\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle \left|0\right\rangle \pm \left|1\right\rangle \left|1\right\rangle )$ and $\left|{{{\Psi }}}^{\pm }\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle \left|1\right\rangle \pm \left|1\right\rangle \left|0\right\rangle )$. Since a simple local operation such as a single qubit X or Z gate can transform Bell states from one to another, this provides us the freedom of switching the states at low cost. Different Bell states or states with different entanglement entropy might serve as identities (ID) for entangled pairs for further usages in the network layer⁸. In reality, the bipartite states between adjacent nodes are non-maximally entangled states, characterized by their entanglement fidelity. To ensure this fidelity is above a certain threshold F_th, the network is initialized by quantum entanglement purification on each edge, which results in a reduced number of shared entanglement pairs, thus a reduced edge capacity. We assume the fidelities of multiple entangled pairs along the same edge to be identical while the fidelities on different edges can vary, as influenced by various factors such as geographical constraints or human interventions. The average entanglement fidelity of a certain edge can be calculated by pre-characterization; here we assume the fidelities on all edges to follow a normal distribution N(F_mean, F_std). Note we take the fidelity to be one if it exceeds unity.

At the start of a time window, a set R of simultaneous connection requests are received. Each request r ∈ R requires the generation of at least ${\bar{f}}^{r}$ entangled pairs between two remote nodes (denoted source node and terminal node) by implementing entanglement swapping (see Fig. 1a) along a given path. Local entanglement swapping operations at quantum stations are imperfect, with a probability of success p_in ∈ (0, 1). This implies that the time needed to successfully entangle two remote stations along a certain path will grow exponentially with increasing path length, an important aspect in evaluating routing performances (see following sections). An optical link between two nodes will be successfully established with probability p_out, mainly limited by optical loss during the long-distance transmission. We assume homogeneous p_in and p_out on all network nodes and edges in simulations. We assumed first-generation quantum repeaters, that is, heralded entanglement generation (purification) is applied on the repeaters and quantum error correction (QEC) procedures are not available to suppress the errors. Still, our model could easily be generalized to second- or third-generation repeaters, where QEC is used to replace the heralded entanglement generation (purification). This would greatly enhance the network performance, as described by the parameters p_in, p_out. In addition, the QEC protocol only needs one-way signaling and would allow higher communication rates between quantum stations.

With these preliminaries, we define the routing problem on small-capacity regular (lattice) quantum networks as the following:

Given a quantum network with non-uniform edge capacity and variable topology due to imperfect initialization and limited quantum memory on stations, design an effective algorithm that provides routing solutions to arbitrary entangled-pair requests, able to ensure above-threshold entanglement fidelity and to process multiple connection requests during the same time window.

To efficiently utilize network resources within each processing window, multiple connection paths L^r are identified and established for each request r, as opposed to only using the single shortest path between the request pair. Specifically, the solution scheme determines the flow (allocated capacity) ${f}_{ij}^{r,l}$ of each path l for each connection request r, on every edge (i, j) in the network, such that the aggregated flow of each request ${f}^{r}={\sum }_{l\in {L}^{r}}{f}^{r,l}$ is able to meet the demand ${\bar{f}}^{r}$ to a sufficient extent.

This problem formulation considers multiple paths on the network for a specific connection request, as opposed to only utilizing the (single) shortest path as in most virtual circuit routing schemes²³. We do not aim at a multi-commodity flow optimization for routing²⁴, since the optimization is NP-hard when relaxing the shortest path constraint. Although an optimal solution for ${f}_{ij}^{r,l}$ is not derived here, we strive to provide efficient solutions for this routing task through sophisticated algorithmic design. Note that the queuing process on each node (station) is not considered in this study, which deals with arranging connection requests over sequential processing windows; the current scheme provides routing solutions within each processing window, assuming that a certain number of requests are processed in the same batch upon submission.

Routing scheme

Our stepwise routing scheme consists of both physical steps (in which quantum operations are physically conducted) and algorithmic steps (in which computations are performed). The overall scheme, summarizing both computational instructions and physical operations (text in red), is shown in Fig. 2.

Fig. 2: Illustration of the routing protocol.

Physical steps (in which quantum operations are physically conducted) are shown in red.

At the start of each processing window (Step 0), the quantum network G = (V, E) is reinitialized. The maximal edge capacity is C₀ on all edges. Entanglement generation is attempted between adjacent nodes. Since the entanglement generation probability p_out is less than one, the realized capacity on any edge is always less than C₀. Multiple transmission requests R = {r} are received. Each request consists of one source and one terminal node (r = [S_r, T_r]), the minimum demand of entanglement pairs ${\bar{f}}^{r}$, along with a weight factor w_r. There is no restriction on the choice of source/terminal nodes and the protocol supports all possible scenarios, including same S, same T, same [S, T].

At Step 1, entanglement purification is carried out on each edge (i, j) ∈ E having fidelity below the threshold F_th and a realized edge capacity (i.e., number of entangled pairs) C_ij ≤ C₀. The initial edge fidelity (normally distributed at N(F_mean, F_std)) and the probability of successful entanglements between adjacent stations p_out determine C_ij. Note the value of F_th may vary in practice for different network functionalities. To ensure enough bandwidth for each connection path, we apply a cap l_max to the number of possible paths traversing a single edge. Edges with residual capacity C_ij smaller than l_max are deactivated (see Fig. 3a). This ensures that the minimum allocated flow for a single path f_min (of a certain request), is always no less than one:

$${f}_{{\mathrm{min}}}={\rm{floor}}\left(\frac{\min ({C}_{ij})}{{l}_{{\mathrm{max}}}}\right)\ge \frac{{l}_{{\mathrm{max}}}}{{l}_{{\mathrm{max}}}}=1.$$

(1)

Fig. 3: Illustration of the routing protocol.

a Initialization of network topology. On a specific edge, purification realizes one entanglement pair out of eight available entangled pairs (C_ij = 1, C₀ = 8), which falls below the maximum number of paths l_max allowed on each edge. To ensure that each path has at least one channel allocated, this edge with insufficient capacity is then deactivated (indicated by the red bar). b. A sample routing scenario. Two connection requests (r₁: S₁ ↔ T₁; r₂: S₂ ↔ T₂) are received; four-shortest paths are identified for each request, utilizing active edges (edges without red bars) on the square lattice network. Each edge may be utilized by multiple paths of a certain connection request, and by multiple requests. Different paths are shown with arrows for clarity, but there is no directionality along the paths. c Capacity allocation scheduling. Three paths for two requests (l₁ for r₁; l₂, l₄ for r₂) utilize the starred edge (in b), on which the three scheduling algorithms (d–f) are illustrated. For proportional share and propagatory update, entangled pairs on this edge are distributed among the three paths through a two-stage allocation: the quota is first determined for each request, then for each path of different requests. In proportional share, the edge capacity is directly allocated; propagatory update calculates the summarized desired capacity on this edge from all paths that utilize it, using the information in the global schedule table, then allocates the unmet capacity demand to these paths. Corresponding deductions are made from the desired flows whose sum exceeds the real edge capacity, and the schedule table is updated at each step. The minimum flow for each path is f_min; the maximum flow deduction for path l of request r is ${f}_{{\mathrm{max}}}^{r,l}-{f}_{{\mathrm{min}}}$, where ${f}_{max}^{r,l}$ is the desired capacity in the global routing table. For progressive filling, f^r,l is 0 on all paths at t = 0 and increases by 1 at each computational interval. At t = 1, the starred edge is saturated and thus the three paths on it are saturated. At t = 2, f^r,l keeps increasing on unsaturated paths.

At Step 2, paths for different connection requests are identified in the revised graph $G^{\prime}$. In order to ensure sufficient redundancy in routing in case of potential network failures, k shortest paths²⁵ are identified between each connection pair r = [S_r, T_r]. The value of k determines how relaxed in length the desired paths are: when k = 1 we only consider a single shortest path; more and longer paths will be utilized under a larger k. A practical and effective value of k should be determined based on specific network conditions, such as the number of requests ∣R∣ allowed within a time window, the size of the lattice network ∣E∣, and the maximum capacity C₀. At minimum, k should be sufficiently large to satisfy the flow demand of each connection request, $k\ {f}_{{\mathrm{min}}}\ge {\bar{f}}^{r}$.

The identified paths are collected in the path information set H = {h_ij}. For each edge (i, j) along each path l identified for a request r, an information entry h_ij is added to the path information set H with the following tuple:

$${h}_{ij}=[r,l,d,o],$$

(2)

where d is the path length and o the order of edge (i, j) in path l.

Step 3 is the core computational procedure of the routing scheme, in which the edge-wise capacity allocation scheduling is performed. In this study, we propose and compare three methods for this scheduling task: (i) proportional share (PS), (ii) progressive filling (PF) and (iii) propagatory update (PU), of which (i) and (ii) are based on well-known scheduling heuristics on classical data networks and (iii) is an algorithm combining the insights of (i) and (ii). Illustrations of the three allocation algorithms are shown in Fig. 3d–f. Below we give a qualitative overview of the three algorithms, whose details could be found in the Supplemental Materials.

In the proportional share method, the scheduling is edge-specific: the edge capacity C_ij is proportionally distributed to all paths that utilize (i, j), in which case only local information on each edge is used. The progressive filling method implements the algorithm in Bertsekas and Gallager²², which guarantees max-min fairness (see sections below). All paths are treated equally, with flows starting at zero and experiencing uniform incremental increase; since in our setting quantum edges have integer capacities, the increment is 1 at each interval. Along the filling process, edges are gradually saturated, and paths utilizing saturated edges stop increasing in flow. Note our integer scheme follows a definition of edge saturation slightly different from that of non-integer flows. In our case, a saturated edge may still have a number of unallocated channels (i.e., the leftovers), but the amount is insufficient to be further allocated. The filling process terminates when no new attempt of flow increments could be realized. Note since flows increase in a fair manner, f_min is not functional in this method.

Combining ideas from these two conventional methods, we propose another method, the propagatory update method, which utilizes a global schedule table and assigns allocation on each edge in a backward, edge-specific manner. The algorithm calculates the summarized desired capacity on each edge from all paths that utilize it, using the information in the global schedule table, then allocates the unmet capacity demand to these paths. This requires making corresponding deductions from the desired flows whose sum exceeds the real edge capacity, and the schedule table is updated at each step. This is similar to the stepwise procedure in the progressive filling method, but there the increments in the schedule table are uniform. Unlike progressive filling, instead of treating all paths equally, proportional share and propagatory update methods differentiate between paths and adopt a similar two-stage strategy: the quota is first determined for each request, then for each path of different requests. The amount of capacities is distributed proportionally at both stages: at the request level, the allocated capacity for each request is proportional to the number of paths of such request that utilize that edge, to the power of β. At the path level, the allocated capacity for each path of a specific request is proportional to its path length, to the power of α. α and β are design features that control the exploitation-exploration tradeoff in path utilization, similar to the idea in ant colonization algorithms²⁶, and essentially determine the fairness of scheduling results. They are set as open parameters (not used in the PF method) whose values are experimented in simulations (see Simulation Results). As mentioned above, before the capacity allocation, the path list L^r going through each edge is truncated to have l_max entries, for the PS and the PU methods. The criterion for truncation is the path length: keep short paths in the list and remove long paths; a path is always kept in the list if it is the sole path for a certain request. Details of the three scheduling methods are explained in Supplemental Materials.

The final allocated capacity flow of each path is determined at Step 4. The short-board constraint is applied: for path l of request r, the final flow f^r,l is determined by the minimum allocated capacity for l among the values on all the edges in this path:

$${f}^{r,l}=\mathop{\min }\limits_{l\in {L}^{r}}[\,{C}_{ij}^{r,l}],\quad \,\text{for}\,\,(i,j)\in l.$$

(3)

where ${C}_{ij}^{r,l}$ is determined at Step 3. Note this constraint is only necessary if proportional share scheduling is used at Step 3; for both progressive filling and propagatory update, the constraint is already implied during the allocation process.

Step 2–4 complete the algorithmic computation of the routing scheme. Based on the determined routing schedule output from Step 4, local quantum operations (e.g., entanglement swapping) are conducted accordingly and scheduled remote entanglements are established (Step 5). The realized flow for each request ${f}^{r}={\sum }_{l\in {L}^{r}}{f}^{r,l}$ is compared with the demand ${\bar{f}}^{r}$; unsatisfied requests are queued to the next processing window.

Performance measures

To evaluate the performance of our routing scheme, we consider three performance measures targeting the three features of our routing design (multi-request, multi-channel, and multi-path). In line with the performance evaluation of classical data networks, these measures characterize key properties in routing: throughput, traffic and delay. We also introduce metrics that characterize the fairness of scheduling. These measures (Table 1) target at different aspects of the routing task and are useful figures of merit in quantum network applications. Note entanglement fidelity is not considered among performance measures since our routing scheme ensures that the fidelity is always above the desired threshold.

Table 1 Evaluation of routing performance.

Throughput – Besides fidelity, entanglement generation rate is another critical quantity typically used to evaluate the performance of quantum networks. In the current setting, the entanglement generation rate corresponds to the number of entangled pairs in the network that are successfully established during the fixed time window; in routing terminology, this is known as the throughput of the system. Considering the weights of different connection requests, we define system throughput as the total weighted flow aggregating over all paths and all requests:

$$F=\sum _{r}{w}_{r}\sum _{l}{f}^{r,l}{p}_{{\mathrm{in}}}^{{d}_{r,l}-1}$$

(4)

Note this definition of throughput is slightly different from that on classical data networks due to a non-negligible possibility of failure (i.e. p_in < 1) during internal connections at each station (e.g., entanglement swapping).

Since our routing task is not a multi-commodity flow optimization problem, it is not guaranteed that requested demand ${\bar{f}}^{r}$ could always be satisfied. Therefore, it is desired in certain cases to ask to maximize the minimum flow of all requests, in which case we could use the alternative metric instead of F to evaluate system throughput: the minimum flow ${F}_{{\mathrm{min}}}=\mathop{\min }\nolimits_{r}{w}_{r}{\sum }_{l}{f}^{r,l}{p}_{{\mathrm{in}}}^{{d}_{r,l}-1}$. Tests suggest that in practice F and F_min are almost always positively correlated and thus could be used interchangeably. We thus keep F as the measure for throughput. As mentioned, throughput (of a single time window) is a straightforward figure of merit in quantum network applications (e.g., the key generation rate in quantum key distribution.

Traffic – To evaluate the amount of routed traffic on the network, we calculate the utilization u_ij of available capacity on each edge (i, j):

$${u}_{ij}=\frac{{\sum }_{r,l}{f}_{ij}^{r,l}}{{C}_{ij}}\in (0,1].$$

(5)

The overall traffic condition could be signaled via the mean U_ave and variance U_var of the utilization factors u_ij on all utilized edges. For an efficient routing performance, it is desired that the overall capacity utilization U_ave is high, i.e., little idleness, while the traffic is evenly distributed without the existence of many bottleneck edges, i.e., U_var is small.

Delay – To preserve sufficient transmission redundancy in routing, multiple paths of various length are exploited for each connection request. For each request r, we calculate the path length stretching factor γ_r, which is defined as the average length of all paths for this request (weighted by the flow), normalized by the shortest path length d_r,0:

$${\gamma }_{r}=\frac{{\sum }_{l}{f}^{r,l}{d}_{r,l}}{{d}_{r,0}{\sum }_{l}{f}^{r,l}},$$

(6)

where d_r,l denotes the path length for path l under request r. The average stretching factor γ of the system is calculated from the γ_r of all requests; γ_r (and thus γ) is always no less than 1. In most cases, quantum connections take nontrivial processing time during each hop on the path, hence longer paths can induce more delay in entanglement generation. If one assumes the same processing time on each edge in the network, then γ indicates the (relative) average delay of our routing results: γ = 1 corresponds to the situation where all flows take the shortest path, and thus the routing has minimum delay; a larger γ indicates a higher delay where circuitous paths are utilized. Delay may be an important metric in applications such as clock synchronization³.

Fairness – Jain’s index²⁷ is adopted to evaluate the fairness of the scheduling scheme. The total scheduled flow for each request aggregates the amount of all paths, ${f}^{r}={\sum }_{l\in {L}^{r}}{f}^{r,l}$, and the fairness of scheduling over requests is thus given by:

$${J}_{{\mathrm{req}}}=\frac{{({\sum }_{r\in R}{w}_{r}{f}^{r})}^{2}}{| R| {\sum }_{r\in R}{({w}_{r}{f}^{r})}^{2}}.$$

(7)

J_req falls between [0, 1] with J_req = 1 representing complete fairness. Evidently, the progressive filling algorithm obtains the highest fairness (J_req ≈ 1) among the three capacity allocation methods, guaranteeing max-min fairness²⁸; values of α and β in proportional share and propagatory update algorithms affect their fairness, which is often substantially below 1 for these two methods. A large J_req ensures that connection requests within a processing window are processed in a relatively fair manner, which is clearly desirable. In a way similar to equation (7), one could also calculate the fairness index with respect to each path, J_path:

$${J}_{{\mathrm{path}}}=\frac{{({\sum }_{r\in R}{w}_{r}{\sum }_{l\in {L}^{r}}{f}^{r,l})}^{2}}{| R| {\sum }_{r\in R}{w}_{r}^{2}{\sum }_{l\in {L}^{r}}{({f}^{r,l})}^{2}}.$$

(8)

A high fairness of flows on different paths is also desirable, in which case one avoids the situation where projected flows are concentrated on a small number of paths. As one would imagine, the routing will be less robust to potential network failures if one or few paths dominate the flow.

Parameter determination

At the start of each processing window, new connection requests R are received, and the network is reinitialized with edge capacities C_ij reset according to entanglement purification results. System parameters (X = {l_max, k, α, β} for PS and PU, and X = k for PF) need to be determined specifically for the current time window. As one would imagine, parameters are chosen so as to optimize a desired objective function concerning the routing performance of the network, which could be constructed from the performance measures discussed above. The specific form of the objective function could be determined according to specific requirements of a given application. For example, a general-form objective function may simultaneously consider the throughput F, traffic (in terms of U_ave and U_var), and delay γ of routing results, using π₁, π₂, π₃ to denote the relative weight of each measure. The corresponding optimization problem could then be formulated as

$$\begin{array}{ll}{X}^{* }&= \mathop{\mathrm{arg}\; \mathrm{max}} \limits_{\{{l}_{{\mathrm{max}}},k,\alpha ,\beta \}}F+{\pi }_{1}{U}_{{\mathrm{ave}}}-{\pi }_{2}{U}_{{\mathrm{var}}}-{\pi }_{3}\gamma \\ s.t.&\hspace{0.17em}G^{\prime} ,R,{C}_{ij}\ (i,j)\in E^{\prime} \\ &\hspace{0.17em}{l}_{{\mathrm{max}}},k\in {{\mathbb{Z}}}^{+}\end{array}$$

(9)

As one could see, the objective function is flexible and may contain multiple terms, instead of using the throughput or delay as the sole objective. Note the above optimization problem is distinct from the multi-commodity flow problem in optimal routing on traditional data networks. Requested demands ${\bar{f}}^{r}$ do not serve as constraints of the problem, and in our setting we allow that some demands are unmet. The queuing process and the weighting mechanism are designed to deal with unsatisfied demands. Depending on the computational capacity of the scheduler (the central processor), this optimization could be solved either through brute force searching over {l_max, k, α, β} (thanks to the relatively small degree of freedom), or by applying some machine learning techniques. For example, one could use supervised learning or reinforcement learning, where the connection requests R and the weighted adjacency matrix of the realized graph $G^{\prime}$ are input, and the learned parameters X^* are output. Routing performance could be evaluated either in a hard manner (i.e., success/fail, for supervised learning), or in a soft manner (i.e., as rewards, for reinforcement learning). The advantage of using machine learning solvers is that now one could deal with multiple terms in the objective function more flexibly by designing sophisticated learning workflow. Essentially, this allows the learning of high-dimensional properties to evaluate the routing performance, beyond the straightforward performance measures discussed above. Since some key aspects in real quantum network applications are not modeled in the current simulation framework, notably the existence of network failures, it is then desired that an effective machine learning workflow is assembled for the parameter determination of this routing scheme; we leave this question open for future work.

Computational complexity

We briefly discuss the computational complexity of the algorithmic steps in the workflow (i.e., Steps 2–4). Determining the shortest paths incurs the largest computation cost at Step 2, with a time O(∣R∣kV³) = O(∣R∣kE^1.5) for square lattices. Step 4 requires a cost O(∣R∣k) to calculate the allocated capacity for each path. The complexity of Step 3 depends on the specific method. The time is Q_PS = O(E∣R∣l_max) ~ O(E∣R∣k) for proportional share since l_max ~ k, while it is Q_PF = O(C₀) for progressive filling. The complexity of propagatory update is higher due to its iterative nature. In the worst case, the max flow on each path will decrease from the maximum value C₀ to the minimum value f_min step by step. Therefore, for ∣R∣ requests and k paths of each request, the no-improvement counter will be reset to 0 at ∣R∣k(C₀ − f_min) times, resulting in a cost O(∣R∣k(C₀ − f_min)E). Since C₀ − f_min ~ C₀, the complexity of propagatory update is approximately:

$${Q}_{{\mathrm{PU}}} \sim O(E| R| k{C}_{0})={C}_{0}{Q}_{{\mathrm{PS}}},$$

(10)

which is in general the slowest among the three methods. Overall, summarizing the three algorithmic steps, the complexity Q_alg of the scheduler is:

$${Q}_{{\mathrm{alg}}}=O({E}^{1.5}| R| k)+O(E| R| k)+O(| R| k)=O({E}^{1.5}| R| k)$$

for proportional share, O(E^1.5∣R∣k + C₀) for progressive filling, and O((E^0.5 + C₀)E∣R∣k) for propagatory update.

Simulation results

We performed extensive simulations to study the effect of design parameters X = {l_max, k, α, β}, and to demonstrate the robustness of the routing design under different assumptions on entanglement fidelity, F_mean, F_std, F_th, and operation success probabilities p_in, p_out. We characterize the performance of the simulation outcomes from multiple perspectives, using the established metrics: the throughput (total flow F), the traffic (U_ave and U_var), the delay (path stretching factor γ), and fairness over requests (Jain’s index J_req) and paths (J_path). We focus on the comparison among the three scheduling schemes (PS, PF, PU in short). To limit the simulation complexity and better understand system parameters, we consider an 8 × 8 square lattice, with two connection requests [S_i, T_i], i = 1, 2 with same weight and identical request distance. Here the request distance is defined as the Manhattan distance along one direction (the Manhattan distance along the two directions is same in our simulations for simplicity). Under this baseline case, we first demonstrate a sample result of our general routing scheme. Then we study the choice of k, which is used in all three scheduling schemes; tests show that it is the most important design parameter in determining the performances of the three algorithms. Later we study the other three parameters {l_max, α, β} used in PS and PU, with a focus on the fairness of routing as compared to PF which guarantees the max-min fairness. Finally we study the system’s robustness under different conditions of quantum parameters. For each set of parameters, 200 simulation runs are performed, and the results are averaged to account for the stochastic nature in the quantum setup. Beyond the baseline case scenario, alternative network topologies (hexagonal/triangular), arbitrary connection requests (varied request number ∣R∣ and arbitrary distance) and potential network failures (edge/node failure) are studied in further simulations.

Baseline case. In Fig. 4, we demonstrate a sample result of our routing scheme. Initially, C₀ = 100 entangled pairs are prepared at each station. After entanglement purification (Step 1), 106/112 edges in the 8 × 8 square lattice are maintained, under quantum parameters {F_mean, F_std, F_th, _pin, p_out} = {0.9, 0.9, 0.8, 0.1, 0.8} (left, Fig. 4a). Two connection requests ([33, 66], [63, 36]) are received, with source/terminal nodes shown in red/blue; the first/second coordinate indicates the horizon/vertical axis (see node 71 in Fig. 4a). System parameters are X = {l_max, k, α, β} = {10, 10, 1, 1}. Ten paths are identified for each request (Step 2); after Step 3 and Step 4, the routing results under three scheduling schemes are compared. Figure 4b shows the traffic on the network in a graphic view (left). We compare performance measures of the three scheduling algorithms (see also Table. 1): PU obtains the largest throughput, and it best exploits edge capacities; indeed, it shows that the scheduled flows on paths are almost always the highest on PU (right top, Fig. 4a, so are the capacity utilizations on different edges (Fig. 4c). PS obtains the smallest variance in edge capacity utilizations, suggesting that the routed traffic is more evenly distributed in PS than in PU or PF; yet PS has the poorest throughput F and average capacity utilization U_ave. PF has less throughput and capacity utilization than PU, but as expected, the scheduling is completely fair, with respect to both requests (J_req) and paths (J_path). PU is the least fair scheme among the three and it can be attributed to the large flow on few paths (e.g., f_1,6, f_1,7, f_2,8 in Fig. 4a). Various tests are simulated under different parameter sets, and results suggest that the baseline case is representative of the three schemes’ performance; the comparison of performance in Fig. 4b largely hold in an aggregated sense.

Fig. 4: Baseline case results.

a (left) Network topology after entanglement purification; (right) 10 connection paths for each request (bottom) and the allocated flow for each path under the three scheduling schemes (top). Here the nodes are represented by a two digit number and the bottom left corner is denoted as 00. An example of node 71 is labeled in the graph plot. b Comparison of routing performance. Traffic plots (left) and performance measures (right). We show the traffic plot in a 8-by-8 network where edge color and width represent the capacity utilization of the corresponding edge (<30% in green, 30–70% in yellow and >70% in red, large width corresponds to larger utilization). c Capacity utilization on (utilized) edges under the three schemes. For simplicity sake, in all simulations hereafter we set the initial capacity of each edge to be C₀ = 100, and the fidelity distribution among edges follows a normal distribution with mean F_mean = 0.8 and standard derivation F_std = 0.1.

Dependence on request distance and choice of k. In Fig. 5a we show the total flow F of the three algorithms. The throughput, as well as the minimum flow of the two requests, decay exponentially as the distance between request pairs grows. The PU algorithm results in obviously larger throughputs (larger number of entangled pairs), while the other two algorithms are comparable to each other. We notice that the throughput will reach a maximum at moderate k values. This can be explained as slightly higher k values provide more freedom in generating large flows, but beyond the optimum k point there will be more paths along each edge on average, leading to congestion on the utilized edges and resulting in more bottlenecks for each path thus decreasing the throughput. We also observe that with large request distance, k has less of an effect, since there are enough routes to select and less edges where congestion can occur.

Fig. 5: Algorithm performance as a function of number of shortest paths k and request distance.

a Heat map of the throughput F for the two requests. b Routing performance with respect to request distance at k = 10. U_ave, γ, and J_req plots are shown here. c Routing performance with respect to k at request distance 3. U_ave, γ, and J_path plots are shown here. Examples of traffic plots with different parameters for the PU algorithm are shown in the inset of γ plots. The other system parameters are {l_max, α, β} = {15, 1, 0}.

Figure 5b shows the behavior of the other metrics with respect to request distance. As the number of paths between request pairs becomes exponentially large with the request distance, for fixed k the traffic is spread out on all edges of these paths, leading to decreasing capacity utilizations. Similarly, at large request distance, there is no need for the flows to take detours and all utilized paths are indeed shortest paths which yields γ = 1. This is clearly depicted in the traffic plots. We also observe that the PU method is superior in utilizing the edge channels and has better capacity utilizations due to information propagation among different edges during its iterative process. All the algorithms demonstrate excellent performance in dealing with multiple requests. In particular, the PF algorithm, due to its step-by-step filling nature, performs excellently in balancing the requests and paths.

For fixed requests as shown in Fig. 5c, choosing a larger k means that the routing algorithms tend to explore more edges, which results in a lower average capacity utilization. On the same note, circuitous paths will be utilized in routing, which increases the normalized path length thus the time delay. Meanwhile, for the PS and PU algorithm, the flow variance among different paths will increase, leading to decreasing fairness over paths. These results point out that the parameter k is crucial in determining path properties.

Effect of fidelity threshold. Finally, we discuss the fidelity threshold that can affect the entanglement purification steps (thus the realized capacity C_ij). Specific tasks in quantum network would demand different error rates or fidelity thresholds and the corresponding entanglement purification will modify the topology of the network in different ways. In Fig. 6 we show the dependence of the protocol performance on fidelity threshold. As the fidelity bound raises, more purification steps are needed, monotonously decreasing the edge capacity and hence the throughput. Intuitively, one might expect that for high fidelity threshold, in general edges will have less realized capacity C_ij which can be fully utilized, leading to large capacity utilization. However, as shown in Fig. 6a, the average capacity utilization follows the same trend as the throughput. This is due to the fact that for fixed k, the edge removal due to repeated purification steps will force the routing scheme to explore more edges in the network thus decreasing the overall capacity utilization. This is clearly shown in the traffic plots (Fig. 6b). Similarly, for high fidelity threshold, the normalized path length is clealy larger than unity for the three algorithms and the flow among different paths tends to have large variance, thus small fairness over paths for PS and PU (Fig. 6d). Nevertheless, the two requests are well balanced with high fairness over request for all allocation algorithms (Fig. 6d).

Fig. 6: Protocol performance with respect to fidelity threshold.

a Total flow and average capacity utilization. Inset shows the minimum flow of the two requests. b Normalized path stretching factor. Traffic plots at two extreme case for the propagatory update algorithm are presented. c, d Fairness over paths (c) and requests (d). The fidelity distribution among edges follow the normal distribution N(0.8, 0.1) and the request distance is fixed to be 3 here. The other system parameters are {l_max, α, β} = {15, 1, 0}.

Potential network failures. One critical feature of our routing scheme is multi-path, and the claim is that by utilizing more than one path, the routing will be more robust to potential network failures. The network failures can be induced by the breakdown of a central station, interruption of the signal transmission on physical channels, or other adversary situations in the real world. We simulate both edge failures (an edge is dead) and node failures (a station is dead; all edges linked to it are dead) to test the scheme’s robustness (Fig. 7). These two failure modes are among the most common network issues, which may also take place due to security concerns (such as external eavesdroppers). The system throughputs F before and after the failure are compared for each scheduling scheme, under different failure modes (1–4 edges failure, 1–4 nodes failure; edges and nodes are chosen from those being utilized). 20 simulations are averaged at each data point under baseline case parameters (see Fig. 7). Results show that, as expected, as the failure mode gets more and more serious, the system achieves smaller and smaller throughput, but is still working; after the shutdown of 4 out of the 16 utilized stations, the system still maintains some outputs. We also notice that of the three schemes, PS shows the greatest robustness, slightly greater than PF, whereas PU’s superiority in throughput F gradually vanishes in face of network failures. Similar robustness conditions are identified on other performance measures (see Supplemental Material).

Fig. 7: Robustness of routing results against network failures.

Comparing system throughput before and after the failure of the three scheduling schemes. Different failure modes (1–4 edges failure, 1–4 nodes failure) are simulated.

Number of requests per window. Within each processing window, we simulate 2-10 random connection requests (arbitrary [S, T] pairs) and compare routing performances (Fig. 8). 20 simulations are averaged at each data point under based case parameters (see Fig. 3). With ∣R∣ increasing, the system becomes more crowded: F goes up whereas F/∣R∣ goes down, but the degradation curvature is better than inverse-proportional (blue line); the superiority of PU in throughput is always maintained. Meanwhile, the network traffic is more diluted, and the routing less fair for PU and PS, with U_ave, U_var, J_req, and J_path falling quasi-linearly. There is no consistent change in average routing delay γ; PU seems to produce less delayed routing under more requests, but the result is not significant.

Fig. 8: Performance under different number of requests (2–10) per window.

a Throughput F and normalized throughput F/∣R∣; blue curve shows the reference line 60/∣R∣. b Traffic mean U_ave and variance U_var (which is shown as the error bars with reduced scale of factor 2). c Delay γ. d Fairness J_req and J_path.

Discussion

We benchmarked the performance of the routing scheme under different parameter regimes. Here we highlight differences in resource allocation for the three scheduling schemes. Performance results show that the three schemes have different advantages: progressive filling is the fairest method, whereas the fairness of the two proportional methods is compromised to a nontrivial extent, and depends on the system parameters α, β. In terms of system throughput and capacity utilization, the new propagatory update scheme stands out by a large margin, and the superiority is largely maintained under all network conditions, even in face of network failures. However, as a tradeoff, the increased throughput are not attributed to all requests in a fair manner, and propagatory update routing results demonstrate the largest variance on edge utilizations as well. The least efficient scheme is proportional share, which generates the least throughput. However, the variance of edge utilization is smaller than in propagatory update, and it is more robust against network failures. This suggests that this scheme utilizes network resources in the most economical way. Also, since a global information table is not maintained (hence not subject to errors) and proportional allocations are performed only at the local scale, the proportional share may also be the most robust scheme against network errors on top of failures.

We now proceed to present the scope of use, limitations and potential future extensions of the routing scheme. We have demonstrated the performance of our routing scheme with a 8 × 8 square lattice network with edge capacity C₀ = 10² and <10 requests per time window. In reality, the implementation scale of quantum networks will be determined by various physical, geological and economic constraints. Current lab-scale quantum networks are very small (~2 × 2) with very limited edge capacity C₀ (only few qubits), since the preparation of entangled pairs is extremely costly; for our routing scheme to be put in use, huge leaps in quantum engineering are necessary. Practically, the lattice size and edge capacity should be decided by the specific functionality of the quantum network, and the number of requests being processed within a time window are determined by service considerations. Also note that alternative lattice topologies (e.g., hexagonal, triangular) could be experimented in real applications; current results apply to square lattice, yet it is believed that similar results could be obtained on other common regular lattice structures.

We further note that, in the space domain, we are assuming a central processor in the network and global link-state information is broadcast to each node. Under restricted cases, however, only local link-state knowledge (link with the nearest neighboring nodes) is available at each node. For example, as the size of the network G(V, E) increases, the classical communication time is non-negligible and can be far beyond the quantum memory lifetime. In this scenario, instead of finding the paths with a global processor, one can perform entanglement swapping on two local quantum memories in a way such that the sum of their distance to the request pair can be minimized, as shown in Pant et al.²¹. However, in a more complex quantum network where multi-request, multi-path and multi-channel are involved, searching for an efficient routing strategy remains elusive and might be interesting for future study.

In the time domain, the current protocol is used for processing a certain number of connection requests within one active time window; it is expected that a queueing model²⁹ might be constructed to tackle the network functioning beyond the processing time window. Such queueing system should provide guidelines for coordinating the reception of incoming connection requests with the recycling of entangled pairs, in which case, processing windows could essentially overlap, and one does not need to wait for the end of one batch of requests before starting the next window. In this scenario, other concerns in routing design might arise, for example, dealing with network congestions, e.g. subsequent re-distribution of capacities after initial allocation³⁰. Since these issues have been intensively studied in classical network, discussions on such high-level infrastructures of the current protocol are not included in this paper and are left for future studies.

Next we point out that in the above protocol we consider entanglement purification only at the first step, that is, only between adjacent nodes. As successive entanglement swapping operations are imperfect, they might degrade the fidelity of generated remote entanglement. To overcome this drawback, one can adopt a nested protocol^14,20 where repeated purification is performed after each entanglement swapping step to ensure that the remote entangled states have regained a sufficiently large fidelity. Then an updated version of the routing scheme in which the resource consumption during successive entanglement purification is taken into account might be designed.

Finally, while here we consider entanglement between two nodes, i.e., Bell states, an extension to GHZ states and local GHZ projection measurement might bring advantages in generating remote entanglement^31,32,33,34. For example, even if the GHZ states are more difficult to prepare and more fragile to environment noise, they provide more configurations on a quantum network, thus creating more complex topology which can be unreachable for Bell states. The compromise between this gain and its cost can in principle benefit our entanglement routing designs. Similarly, the GHZ projection measurement in a local station can glue more than two remote stations together and modify the network topology. The routing strategy that utilize these operations will be an interesting topic to study, both mathematically and physically.

In conclusion, we have proposed an efficient protocol that tackles the routing problem on quantum repeater networks. We have shown that entanglement purification, which increases entanglement fidelity, can modify the network topology and affect the following routing design. For general multi-request, multi-path, and multi-channel problems, we developed three algorithms that can allocate limited resource to efficiently generate entangled pairs between remote station pairs.

Among the first attempts to tackle this complex problem, our routing scheme provides a solution to exploit the full capability of complex quantum networks, where efficient entanglement generation of remote station pairs are desired. The routing design here may also inspire future work that combine the quantum information science with classical network theory.